


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Характеристическое уравнение
Определение "Характеристическое уравнение" в Большой Советской Энциклопедии
Характеристическое уравнение в математике,
1) Характеристическое уравнение матрицы - алгебраическое уравнение вида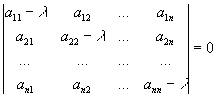 ;
;
определитель, стоящий в левой части Характеристическое уравнение, получается из определителя матрицы А = ||aik||n1 вычитанием величины l из диагональных элементов. Этот определитель представляет собой многочлен относительно Х - характеристический многочлен. В раскрытом виде Характеристическое уравнение записывается так: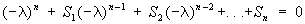 ,
,
где S1 = a11 + a22 +... ann - т. н. след матрицы, S2 - сумма всех главных миноров 2-го порядка, т. е. миноров вида 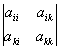 (i < k) и т.д., а Sn - определитель матрицы А. Корни Характеристическое уравнение l1, l2,..., ln называются собственными значениями матрицы А. У действительной симметричной матрицы, а также у эрмитовой матрицы все lk действительны, у действительной кососимметричной матрицы все lk чисто мнимые числа; в случае действительной ортогональной матрицы, а также унитарной матрицы все |lk| = 1.
(i < k) и т.д., а Sn - определитель матрицы А. Корни Характеристическое уравнение l1, l2,..., ln называются собственными значениями матрицы А. У действительной симметричной матрицы, а также у эрмитовой матрицы все lk действительны, у действительной кососимметричной матрицы все lk чисто мнимые числа; в случае действительной ортогональной матрицы, а также унитарной матрицы все |lk| = 1.
Характеристическое уравнение встречаются в самых разнообразных областях математики, механики, физики, техники. В астрономии при определении вековых возмущений планет также приходят к Характеристическое уравнение; отсюда и второе название для Характеристическое уравнение - вековое уравнение.
2) Характеристическое уравнение линейного дифференциального уравнения с постоянными коэффициентами
a0ly (n) + a1y (n-1) +... + an-1y" + any = 0
- алгебраическое уравнение, которое получается из данного дифференциального уравнения после замены функции у и её производных соответствующими степенями величины l, т. е. уравнение
a0ln + a1ln-1 +... + an-1 y" + any = 0.
К этому уравнению приходят при отыскании частного решения вида у = сеlх для данного дифференциального уравнения. Для системы линейных дифференциальных уравнений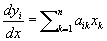 ,
, 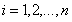 ,
,
Характеристическое уравнение записывается при помощи определителя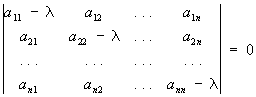
Характеристическое уравнение матрицы A = 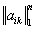 , составленной из коэффициентов уравнений данной системы.
, составленной из коэффициентов уравнений данной системы.
| "БСЭ" >> "Х" >> "ХА" >> "ХАР" >> "ХАРА" |
Статья про "Характеристическое уравнение" в Большой Советской Энциклопедии была прочитана 530 раз
| Коптим скумбрию в коробке |
| Крабы в кокосовом молоке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Периодическая система элементов
- Японское море
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс