


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Штрафных функций метод
Определение "Штрафных функций метод" в Большой Советской Энциклопедии
Штрафных функций метод, метод сведения задач об отыскании условного (относительного) экстремума функций к задачам отыскания безусловного (абсолютного) экстремума. Рассмотрим Штрафных функций метод на примере задач математического программирования. Пусть требуется минимизировать функцию j(х) на множестве X = {x: fi (x) ³ 0, I = 1, 2,... m} n-мерного евклидова пространства. Штрафной функцией, или штрафом (за нарушение ограничений fi (x) ³ 0, i = 1, 2,... m), называют функцию y (х, а), зависящую от х и числового параметра а > 0, обладающую след. свойствами: y(х, а) = 0, если х Î Х и y(х, а) > 0, если x Ï X. Построим функцию M (x, a) = j(x) + y(х, a) и обозначим через x (a) любую точку её безусловного глобального минимума. Пусть 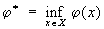 . Функцию y(х, a) выбирают таким образом, чтобы j(x (a))® j* при a ® +¥. В качестве j(х, a) часто выбирают функцию
. Функцию y(х, a) выбирают таким образом, чтобы j(x (a))® j* при a ® +¥. В качестве j(х, a) часто выбирают функцию , q ³ 1.
, q ³ 1.
Выбор конкретного вида функции y(x, a) связан как с проблемой сходимости Штрафных функций метод, так и с проблемами, возникающими при решении задачи безусловной минимизации функции М (х, a).
В несколько более общей постановке Штрафных функций метод заключается в сведении задачи минимизации функции j(х) на множестве Х к задаче минимизации некоторой параметрической функции М (х, a) на множестве более простой структуры с точки зрения эффективности применения численных методов минимизации, чем исходное множество X.
Лит.: Моисеев Н. Н., Элементы теории оптимальных систем, М., 1975; Фиакко А., Мак-Кормик Г., Нелинейное программирование, пер. с англ., М., 1972; Сеа Ж., Оптимизация, пер. с франц., М., 1973.
В. Г. Карманов.
| "БСЭ" >> "Ш" >> "ШТ" >> "ШТР" |
Статья про "Штрафных функций метод" в Большой Советской Энциклопедии была прочитана 391 раз
| Гороховое пюре |
| Гороховое пюре |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Периодическая система элементов
- Японское море
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс