


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Векторное произведение
Определение "Векторное произведение" в Большой Советской Энциклопедии
Векторное произведение вектора а на вектор b — вектор, обозначаемый [а, b] и определяемый так: 1) длина вектора [а, b] равна произведению длин векторов а и b на синус угла j между ними (берётся тот из двух углов между а и b, который не превосходит p), 2) вектор [а, b] перпендикулярен вектору а и вектору b, 3) тройка векторов а, b, [а, b], согласно с ориентацией пространства, всегда правая или всегда левая (см. Векторное исчисление). Векторное произведение широко применяется в геометрии, механике и физике (например, момент силы F, приложенной к точке М относительно точки О, есть Векторное произведение [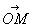 , F]).
, F]).
Лит.; Ильин В. А., Позняк Э. Г., Аналитическая геометрия, М., 1968.
Э. Г. Позняк.
| "БСЭ" >> "В" >> "ВЕ" >> "ВЕК" |
Статья про "Векторное произведение" в Большой Советской Энциклопедии была прочитана 780 раз
| Бургер двойного помола |
| Буддийская молитва в Камбодже |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Объединённая партия гаитянских коммунистов
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная