


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Гамма-функция
Определение "Гамма-функция" в Большой Советской Энциклопедии
Гамма-функция [Г-функция, Г (х)], одна из важнейших специальных функций, обобщающая понятие факториала; для целых положительных n равна Г (n) = (n - 1)! = 1·2... (n - 1). Впервые введена Л. Эйлером в 1729. Гамма-функция-ф. для действительных х > 0 определяется равенством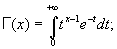
другое обозначение:
Г (х + 1) = p(x) = х!
Основные соотношения для Гамма-функция-ф.:
Г (х + 1) = хГ (х) (функциональное уравнение);
Г (х) Г (1 - х) = p/sin px (формула дополнения);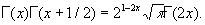
Частные значения: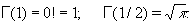
При больших х справедлива асимптотич. Стирлинга формула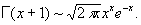
Через Гамма-функция-ф. выражается большое число определённых интегралов, бесконечных произведений и сумм рядов. Гамма-функция-ф. распространяется и на комплексные значения аргумента.
Лит.: Янке Е., Эмде Ф., Таблицы функций с формулами и кривыми, пер. с нем., 3 изд., М., 1959; Фихтенгольц Гамма-функция М., Курс дифференциального и интегрального исчисления, 6 изд., т. 2, М., 1966.
| "БСЭ" >> "Г" >> "ГА" >> "ГАМ" |
Статья про "Гамма-функция" в Большой Советской Энциклопедии была прочитана 798 раз
| Пицца в сковороде |
| Кишки на гриле |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная