


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Гармонические функции
Определение "Гармонические функции" в Большой Советской Энциклопедии
Гармонические функции, функции от n переменных (n ³ 2), непрерывные в некоторой области вместе с частными производными первого и второго порядков и удовлетворяющие в этой области дифференциальному уравнению Лапласа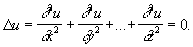
Во многих вопросах физики и механики, где речь идёт о состоянии части пространства, зависящем от положения точки, но не от времени (равновесие, установившееся движение и т. п.), соответствующее состояние представляется Гармонические функции от координат точки. Так, например, потенциал сил тяготения в области, не содержащей притягивающих масс, и потенциал постоянного электрического поля в области, не содержащей электрических зарядов, суть Гармонические функции Точно так же Гармонические функции являются потенциал скоростей установившегося безвихревого движения несжимаемой жидкости, температура тела при условии установившегося распределения тепла, величина прогиба мембраны, натянутой на контур произвольного вида, вообще неплоский (весом мембраны пренебрегают), и т. д.
Наиболее важны для приложения к физике и механике Гармонические функции от трёх переменных (координат точки). В частном случае, когда область пространства ограничена цилиндрической поверхностью, образующие которой параллельны, например, оси z, причём изучаемое явление протекает одинаковым образом в любой плоскости, перпендикулярной к образующим (т. е. не зависит от координаты z), соответствующие Гармонические функции от трёх переменных превращаются в Гармонические функции от двух переменных х и у. Последние находятся в тесной связи с аналитическими функциями f (x) от комплексного переменного x = х + iy. А именно каждая Гармонические функции от х и у есть действительная или мнимая часть некоторой функции f (x), и, обратно, действительная и мнимая части любой аналитической функции суть Гармонические функции от x и у. Например, х2—у2 и 2ху, будучи действительной и мнимой частями функции x2 = х2—у2 + 2ixy, суть Гармонические функции Важнейшими задачами теории Гармонические функции являются краевые, или граничные, задачи, в которых требуется найти Гармонические функции внутри области на основании данных, относящихся к поведению функции на границе этой области. Такова задача Дирихле, где Гармонические функции ищется по её значениям, заданным в точках границы области (например, определение температуры внутри тела по температуре на его поверхности, поддерживаемой так, что она зависит только от точки, но не от времени, или определение формы мембраны по виду контура, на который она натянута). Такова также задача Неймана, где Гармонические функции ищется по величине её нормальной производной, заданной на границе области (например, определение температуры внутри тела по заданному на поверхности градиенту температуры или определение потенциала движения несжимаемой жидкости, обтекающей твёрдое тело, на основании того, что нормальные составляющие скоростей частиц жидкости, прилегающих к поверхности тела, совпадают с заданными нормальными составляющими скоростей точек поверхности тела).
Для решения задач Дирихле, Неймана и др. краевых задач теории Гармонические функции разработаны различные методы, имеющие большое теоретическое значение. Например, для задачи Дирихле известны: альтернирующий метод (Шварца), метод выметания (Пуанкаре), метод интегральных уравнений (Фредгольма), метод верхних и нижних функций (Перрона) и др. При рассмотрении краевых задач для областей общего вида возникают важные вопросы об условиях существования решений, об устойчивости решений при малых изменениях границы области и др. Этим вопросам посвящены работы М. В. Келдыша, М. А. Лаврентьева и др. советских математиков. Весьма большое значение для приложений теории Гармонические функции к задачам физики и техники имеет также разработка методов численного решения краевых задач.
Лит.: Келдыш М. В., О разрешимости и устойчивости задачи Дирихле, «Успехи математических наук», 1940, в. 8; Сретенский Л. Н., Теория ньютоновского потенциала, М.—Л., 1946; Смирнов В. И., Курс высшей математики, 3 изд., т. 4, М., 1957; Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961.
А. И. Маркушевич.
| "БСЭ" >> "Г" >> "ГА" >> "ГАР" >> "ГАРМ" |
Статья про "Гармонические функции" в Большой Советской Энциклопедии была прочитана 846 раз
| Бургер двойного помола |
| Английский рыбный пирог |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Объединённая партия гаитянских коммунистов
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная