


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Грина формулы
Определение "Грина формулы" в Большой Советской Энциклопедии
Грина формулы, формулы интегрального исчисления, связывающие между собой интегралы различных типов. Простейшая из них связывает двойной интеграл по области G с криволинейным интегралом по границе С области G и имеет вид: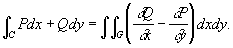
Эта формула была известна ещё Л. Эйлеру (1771). Две другие впервые опубликованы Джорджем Грином в 1828 в связи с исследованиями по теории потенциала: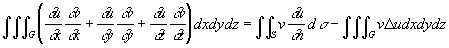
(первая Грина формулы, или предварительная Грина формулы) и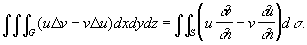
Здесь G - область трёхмерного пространства, поверхность S - граница этой области, Du = ¶2u/¶x2 + ¶2u/¶y2 + ¶2u/¶z2 (аналогично Dv) - оператор Лапласа, ¶u/¶n, ¶v/¶n - производные по направлению внешней нормали к S.
| "БСЭ" >> "Г" >> "ГР" >> "ГРИ" >> "ГРИН" |
Статья про "Грина формулы" в Большой Советской Энциклопедии была прочитана 546 раз
| Бургер двойного помола |
| Английская картошка фри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная