


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Идеал (алгебраич. понятие)
Определение "Идеал (алгебраич. понятие)" в Большой Советской Энциклопедии
Идеал (математический), одно из основных алгебраических понятий. Возникнув первоначально в связи с изучением алгебраических иррациональных чисел, Идеал (алгебраич. понятие) нашли впоследствии многочисленные применения в других отделах математики.
Известно, что всякое целое (рациональное) число можно разложить в произведение простых множителей; например, 60 = 2 · 2 · 3 · 5, причём разложение единственно с точностью до порядка и знака множителей: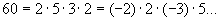

В 19 в. математики столкнулись с необходимостью разлагать на множители числа более общей природы. Если, например, рассматривать числа вида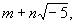
где m и n - любые целые (рациональные) числа, то так же, как и для обычных целых чисел, здесь каждое число всегда можно разложить в произведение далее неразложимых множителей. Однако в этом случае нарушается единственность разложения. Так, число 9 (которое получается, если считать m = 9, n = 0) допускает здесь два различных разложения:
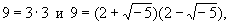
причем ни один из множителей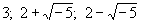
дальше разложить в произведение чисел вида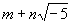
нельзя. Нарушения привычных законов единственности разложения не будет, если свойство делимости связывать не с числами, а с Идеал (алгебраич. понятие) В современной алгебре Идеал (алгебраич. понятие) вводятся в произвольных кольцах. В случае числовых колец (таковым является, например, рассмотренная выше совокупность чисел вида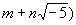
Идеал (алгебраич. понятие) называются также идеальными числами. Идеал (алгебраич. понятие) - это совокупность чисел, принадлежащих данному числовому кольцу (а в случае произвольного кольца - совокупность его элементов), обладающая следующими свойствами: 1) сумма и разность двух чисел (элементов) совокупности принадлежит этой совокупности; 2) произведение числа (элемента) из этой совокупности на любое другое число (на любой другой элемент) кольца также принадлежит этой совокупности. Затем рассматривают вместо чисел соответствующие им Идеал (алгебраич. понятие); так, например, числу 9 соответствует Идеал (алгебраич. понятие) p = (9), состоящий из всех чисел, делящихся на 9.
Числовые понятия, связанные с делимостью чисел, переносятся на Идеал (алгебраич. понятие): один Идеал (алгебраич. понятие) делится на другой, если любой элемент первого лежит также и во втором (для чисел это эквивалентно тому, что любое число первого Идеал (алгебраич. понятие) делится хотя бы на одно число второго); произведение Идеал (алгебраич. понятие) определяется как наименьший Идеал (алгебраич. понятие), содержащий всевозможные попарные произведения элементов из обоих идеалов-множителей; наибольший общий делитель двух Идеал (алгебраич. понятие) - наименьший Идеал (алгебраич. понятие), содержащий элементы как первого, так и второго Идеал (алгебраич. понятие), и др. В совокупности целых чисел любой Идеал (алгебраич. понятие) состоит из кратных какого-либо фиксированного числа: любой Идеал (алгебраич. понятие) является главным. В общем случае, уже для алгебраических иррациональных чисел, не всякий Идеал (алгебраич. понятие) является главным. Делимость на главный Идеал (алгебраич. понятие) эквивалентна делимости на соответствующее этому Идеал (алгебраич. понятие) число. Благодаря наличию не главных Идеал (алгебраич. понятие) для целых алгебраических чисел остаётся справедливой теорема о том, что любой Идеал (алгебраич. понятие) единственным образом разлагается в произведение неразложимых далее Идеал (алгебраич. понятие) Эти неразложимые Идеал (алгебраич. понятие), называются также простыми Идеал (алгебраич. понятие), выполняют роль простых чисел и характеризуются тем, что обязательно содержат хотя бы один из множителей, если они содержат их произведение. Так, в рассмотренном выше примере
(3) = p1 p2,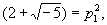
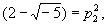
где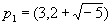
и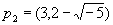
- новые Идеал (алгебраич. понятие), например Идеал (алгебраич. понятие) p1, являющийся наибольшим общим делителем Идеал (алгебраич. понятие)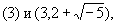
состоит из всех чисел вида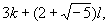
где k и l - любые целые рациональные числа.
Понятие «Идеал (алгебраич. понятие)» (или в первоначальной терминологии «идеального числа») было введено в 1847 для одного частного случая числовых полей немецким математиком Э. Куммером. Строгое и полное обоснование теории Идеал (алгебраич. понятие) для любых числовых полей дали независимо друг от друга немецкий математик Р. Дедекинд в 1871 и русский математик Е. Идеал (алгебраич. понятие) Золотарев в 1877. Новое содержание теория Идеал (алгебраич. понятие) получила в середине 20 в. в связи с развитием общей теории колец.
Лит.: Ван-дер-Варден Б. Л., Современная алгебра, пер. с нем., 2 изд., ч. 1-2, М.-Л., 1947.
| "БСЭ" >> "И" >> "ИД" |
Статья про "Идеал (алгебраич. понятие)" в Большой Советской Энциклопедии была прочитана 1186 раз
| Бургер двойного помола |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная