


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Интегральный логарифм
Определение "Интегральный логарифм" в Большой Советской Энциклопедии
Интегральный логарифм, специальная функция, определяемая интегралом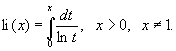
Этот интеграл не выражается в конечной форме через элементарные функции. Если х > 1, то интеграл понимается в смысле главного значения: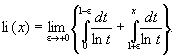
Интегральный логарифм введён в математический анализ Л. Эйлером в 1768. Интегральный логарифм li(x) связан с интегральной показательной функцией Ei(x) соотношением li(x) = Ei(lnx). Для больших положительных х функция li(x) растет как x / lnx. Интегральный логарифм играет важную роль в аналитической теории чисел, так как число простых чисел, не превосходящих х, приблизительно равно li(x).
Лит.: Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968.
| "БСЭ" >> "И" >> "ИН" >> "ИНТ" >> "ИНТЕ" |
Статья про "Интегральный логарифм" в Большой Советской Энциклопедии была прочитана 812 раз
| Пицца в сковороде |
| Бургер двойного помола |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная