Библиотека DJVU
БСЭ
Статистика:
Коши интеграл
Значение слова "Коши интеграл" в Большой Советской Энциклопедии
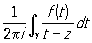,где g - простая замкнутая спрямляемая кривая в комплексной плоскости и f (t) - функция комплексного переменного t, аналитическая на g и внутри g. Если точка z лежит внутри g, то Коши интеграл равен f (z), т. о., любая аналитическая функция может быть посредством Коши интеграл выражена через свои значения на замкнутом контуре. Коши интеграл впервые рассмотрен О. Коши (1831).
Обобщением Коши интеграл являются интегралы типа Коши; они имеют тот же вид, но кривая g не предполагается замкнутой и функция f (t) не предполагается аналитической. Такие интегралы по-прежнему определяют аналитические функции; их значения на g отличаются, вообще говоря, от функции f (t). Систематическое изучение их было начато Ю. В. Сохоцким и впоследствии продолжалось главным образом русскими и советскими математиками (Ю. Г. Колосов, В. В. Голубев, И. И. Привалов, Н. И. Мусхелишвили) как в направлении дальнейших обобщений, так и для приложения к вопросам механики.
Лит.: Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1-2, М., 1967-68; Привалов И. И., Граничные свойства аналитических функций, 2 изд., М.- Л., 1950.
В Большой Советской Энциклопедии рядом со словом "Коши интеграл"
Коши задача | Буква "К" | В начало | Буквосочетание "КО" | Коши неравенствоСтатья про слово "Коши интеграл" в Большой Советской Энциклопедии была прочитана 0 раз
Интересное