


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Лагерра многочлены
Определение "Лагерра многочлены" в Большой Советской Энциклопедии
Лагерра многочлены (по имени французского математика Э. Лагерра, Е. Laguerre; 1834—86), специальная система многочленов последовательно возрастающих степеней. Для n = 0, 1, 2 ... Лагерра многочлены Ln(x) могут быть определены формулой: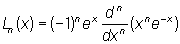 ;
;
в частности:
L0(x) = 1, L1(x) = x - 1, L2(x) = x2 - 4x + 2, L3(x) = x3 - 9x2 + 18x - 6.
Лагерра многочлены ортогональны (см. Ортогональные многочлены) на полупрямой х ³ 0 относительно веса е-х. Дифференциальное уравнение:
ху’’ + (1 — х)у’ + ny = 0.
Рекуррентная формула:
Ln+1(x) = (x - 2n - 1)Ln(x) - n2Ln-1(x).
Лит.: Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М. — Л., 1963.
| "БСЭ" >> "Л" >> "ЛА" >> "ЛАГ" |
Статья про "Лагерра многочлены" в Большой Советской Энциклопедии была прочитана 469 раз
| Бургер двойного помола |
| Крабы в кокосовом молоке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Периодическая система элементов
- Японское море
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс