


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Ортогональные многочлены
Определение "Ортогональные многочлены" в Большой Советской Энциклопедии
Ортогональные многочлены, специальные системы многочленов {рп (х)}; n = 0, 1, 2,..., ортогональных с весом r(х) на отрезке [а, b ] (см. Ортогональная система функций). Нормированная система Ортогональные многочлены обозначается через 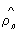 , а система Ортогональные многочлены, старшие коэффициенты которых равны 1,— через
, а система Ортогональные многочлены, старшие коэффициенты которых равны 1,— через 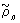 . В краевых задачах математической физики часто встречаются системы Ортогональные многочлены, для которых вес r(х) удовлетворяет дифференциальному уравнению (Пирсона)
. В краевых задачах математической физики часто встречаются системы Ортогональные многочлены, для которых вес r(х) удовлетворяет дифференциальному уравнению (Пирсона)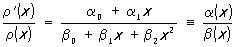
Многочлен рп (х) такой системы удовлетворяет дифференциальному уравнению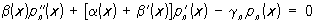
где gn =n [(a1 + (n + 1)b2].
Наиболее важные системы Ортогональные многочлены (классические) относятся к этому типу; они получаются (с точностью до постоянного множителя) при указанных ниже а, b и r(х).
1) Якоби многочлены {Рп (l,m)(х)} — при а = —1, b = 1 r(х) = (1—х)l (1 + x)m, l > —1, m > —1. Специальные частные случаи многочленов Якоби соответствуют следующим значениям l и m: l = m— ультрасферические многочлены 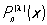 (их иногда называют многочленами Гегенбауэра); l = m = —1/2, т. е.
(их иногда называют многочленами Гегенбауэра); l = m = —1/2, т. е. 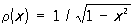 — Чебышева многочлены 1-го рода Tn (x); l = m = 1/2, т. е.
— Чебышева многочлены 1-го рода Tn (x); l = m = 1/2, т. е. 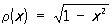 — Чебышева многочлены 2-го рода Un (x); l = m = 0, т. е. r(х) º 1 — Лежандра многочлены Рп (х).
— Чебышева многочлены 2-го рода Un (x); l = m = 0, т. е. r(х) º 1 — Лежандра многочлены Рп (х).
2) Лагерра многочлены Ln (x) — при а = 0, b = + ¥ и r(х) = е—х (их наз. также многочленами Чебышева — Лагерра) и обобщённые многочлены Лагерра 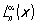 — при
— при 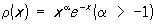 .
.
3) Эрмита многочлены Нn (х) — при а = —¥, b = + ¥ и 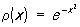 (их называют также многочленами Чебышева — Эрмита).
(их называют также многочленами Чебышева — Эрмита).
Ортогональные многочлены обладают многими общими свойствами. Нули многочленов рn (х) являются действительными и простыми и расположены внутри [а, b ]. Между двумя последовательными нулями многочлена рn (х) лежит один нуль многочлена pn+1 (х). Многочлен рn (х) может быть представлен в виде т. н. формулы Родрига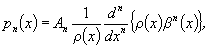
где An — постоянное, а b(х) см. формулу (*). Каждая система Ортогональные многочлены обладает свойствами замкнутости. Три последовательных Ортогональные многочлены 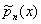 ,
, 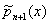 ,
,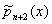 связаны рекуррентным соотношением:
связаны рекуррентным соотношением: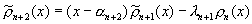 ,
,
где ап+2 и ln+2 следующим образом выражаются через коэффициенты этих многочленов: если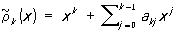 ,
,
то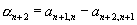 ;
;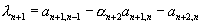
Общая теория Ортогональные многочлены построена П. Л. Чебышевым. Основным аппаратом изучения Ортогональные многочлены явилось для него разложение интеграла 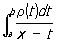 в непрерывную дробь с элементами вида х — an и числителями ln—1. Знаменатели jn (х)/рn (х) подходящих дробей этой непрерывной дроби образуют систему Ортогональные многочлены на отрезке [a, b ] относительно веса r(х).
в непрерывную дробь с элементами вида х — an и числителями ln—1. Знаменатели jn (х)/рn (х) подходящих дробей этой непрерывной дроби образуют систему Ортогональные многочлены на отрезке [a, b ] относительно веса r(х).
Приведённые выше классические системы Ортогональные многочлены выражаются через гипергеометрическую функцию.
Лит.: Сеге Г., Ортогональные многочлены, пер. с англ., М., 1962; см. также лит. при ст. Ортогональная система функций.
В. И. Битюцков.
| "БСЭ" >> "О" >> "ОР" >> "ОРТ" |
Статья про "Ортогональные многочлены" в Большой Советской Энциклопедии была прочитана 987 раз
| Бургер двойного помола |
| Бургер двойного помола |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная