


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Лагранжа метод множителей
Определение "Лагранжа метод множителей" в Большой Советской Энциклопедии
Лагранжа метод множителей, метод решения задач на условный экстремум; Лагранжа метод множителей заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — т. н. функции Лагранжа.
Для задачи об экстремуме функции f (х1, x2,..., xn) при условиях (уравнениях связи) ji(x1, x2, ..., xn) = 0, i = 1, 2,..., m, функция Лагранжа имеет вид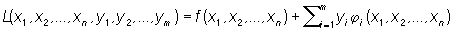 .
.
Множители y1, y2, ..., ym наз. множителями Лагранжа.
Если величины x1, x2, ..., xn, y1, y2, ..., ym суть решения уравнений, определяющих стационарные точки функции Лагранжа, а именно, для дифференцируемых функций являются решениями системы уравнений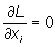 , i = 1, …, n;
, i = 1, …, n; 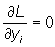 , i = 1, …,m,
, i = 1, …,m,
то при достаточно общих предположениях x1, x2, ..., xn доставляют экстремум функции f. Функция Лагранжа L применяется также при исследовании задач вариационного исчисления и математического программирования. Впервые Лагранжа метод множителей был предложен в 1797 Ж. Лагранжем в связи с задачами дифференциального исчисления.
Лит.: Кудрявцев Л. Д., Математический анализ, т. 2, М., 1970.
| "БСЭ" >> "Л" >> "ЛА" >> "ЛАГ" |
Статья про "Лагранжа метод множителей" в Большой Советской Энциклопедии была прочитана 454 раз
| Коптим скумбрию в коробке |
| Вкуснейшие куриные леденцы |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Периодическая система элементов
- Японское море
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс