Линза (в оптике)

Определение "Линза (в оптике)" в Большой Советской Энциклопедии

Линза. Рис.

Линза (нем. Linse, от лат. lens - чечевица), прозрачное тело, ограниченное двумя поверхностями, преломляющими световые лучи; является одним из основных элементов оптических систем. Наиболее употребительны Линза (в оптике), обе поверхности которых обладают общей осью симметрии, а из них - Линза (в оптике) со сферическими поверхностями, изготовление которых наиболее просто. Менее распространены Линза (в оптике) с двумя взаимно перпендикулярными плоскостями симметрии; их поверхности цилиндрические или тороидальные. Таковы Линза (в оптике) в очках, предписываемых при астигматизме глаза, Линза (в оптике) для анаморфотных насадок и т. д.

Линза. Рис.

Материалом для Линза (в оптике) чаще всего служит оптическое и органическое стекло. Специальные Линза (в оптике), предназначенные для работы в ультрафиолетовой области спектра, изготовляют из кристаллов кварца, флюорита, фтористого лития и др., в инфракрасной - из особых сортов стекла, кремния, германия, флюорита, фтористого лития, йодистого цезия и др.

Описывая оптические свойства осесимметричной Линза (в оптике), обычно рассматривают лучи, падающие на неё под малым углом к оси, составляющие т. н. параксиальный пучок лучей. Действие Линза (в оптике) на эти лучи определяется положением её кардинальных точек - т. н. главных точек Н и H", в которых пересекаются с осью главные плоскости Линза (в оптике), а также переднего и заднего главных фокусов F и F" (рис. 1). Отрезки HF = f и H"F" = f" наз. фокусными расстояниями Линза (в оптике) (в случае, когда среды, с которыми граничит Линза (в оптике), обладают одинаковыми показателями преломления, f всегда равно - f’); точки О пересечения поверхностей Линза (в оптике) с осью называются её вершинами, расстояние между вершинами - толщиной Линза (в оптике)

Геометрические величины, характеризующие отдельные Линза (в оптике) и системы Линза (в оптике), принято считать положительными, если направления соответствующих отрезков совпадают с направлением лучей света На рис. 1 лучи проходят через Линза (в оптике) слева направо, и так же ориентирован отрезок H"F". Поэтому здесь f’ > 0, a f < 0.

Преломления на поверхностях Линза (в оптике) изменяют направления падающих на неё лучей. Если Линза (в оптике) преобразует параллельный пучок в сходящийся, её называют собирающей; после прохождения рассеивающей Линза (в оптике) параллельный пучок превращается в расходящийся. В главном фокусе F" собирающей Линза (в оптике) пересекаются лучи, которые до преломления были параллельны её оси. Для такой Линза (в оптике) f’ всегда положительно. В рассеивающей Линза (в оптике) F" - точка пересечения не самих лучей, а их воображаемых продолжений в сторону, противоположную направлению распространения света. Поэтому для них всегда f < 0. В частном случае тонких Линза (в оптике) внешнее отличие собирающих и рассеивающих Линза (в оптике) заключается в том, что у первых толщина краев меньше толщины в центре Линза (в оптике), у вторых - наоборот.

Мерой преломляющего действия Линза (в оптике) служит её оптическая сила Ф - величина, обратная фокусному расстоянию (Ф = 1/f’) и измеряемая в диоптриях (м^-1). У собирающих Линза (в оптике) Ф > 0, поэтому их ещё именуют положительными. Рассеивающие Линза (в оптике) (Ф < 0) называются отрицательными. Употребляют и Линза (в оптике) с Ф = 0 - т. н. афокальные Линза (в оптике) (их фокусное расстояние равно бесконечности). Они не собирают и не рассеивают лучей, но создают аберрации (см. Аберрации оптических систем) и применяются в зеркально-линзовых (а иногда и в линзовых) объективах как компенсаторы аберраций.

Линза (в оптике), ограниченная сферическими поверхностями. Все параметры, определяющие оптические свойства такой Линза (в оптике), могут быть выражены через радиусы кривизны r₁ и r₂ её поверхностей, толщину Линза (в оптике) по оси d и показатель преломления её материала n. Например, оптическая сила и фокусное расстояние Линза (в оптике) задаются соотношением
 (1)

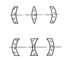
Радиусы r₁ и r₂ считаются положительными, если направление от вершины Линза (в оптике) до центра соответствующей поверхности совпадает с направлением лучей (на рис. 1 r₁ > 0, r₂ < 0). Следует оговорить, что формула (1) верна лишь применительно к параксиальным лучам. При одной и той же оптической силе и том же материале форма Линза (в оптике) может быть различной. На рис. 2 показано несколько Линза (в оптике) одинаковой оптической силы и различной формы. Первые три - положительны, последние три - отрицательны. Линза (в оптике) называется тонкой, если её толщина d мала по сравнению с r₁ и r₂. Достаточно точное выражение для оптической силы такой Линза (в оптике) получают, отбрасывая второй член в (1).

Положение главных плоскостей Линза (в оптике) относительно её вершин тоже можно определить, зная r₁, r₂, n и d. Расстояние между главными плоскостями мало зависит от формы и оптической силы Линза (в оптике) и приблизительно равно . В случае тонкой Линза (в оптике) это расстояние мало и практически можно считать, что главные плоскости совпадают.

Когда положение кардинальных точек известно, положение изображения оптического точки, даваемого Линза (в оптике) (см. рис. 1), определяется формулами:
x·x’ = f·f’ = -f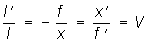’²,
  , (2)

где V - линейное увеличение Линза (в оптике) (см. Увеличение оптическое), l и l" - расстояния от точки и её изображения до оси (положительные, если они расположены выше оси), х - расстояние от переднего фокуса до точки, x" - расстояние от заднего фокуса до изображения. Если t и t" - расстояния от главных точек до плоскостей предмета и изображения соответственно, то (т. к. х = t - f, x" = t’ - f’):
f’/t’ + f/t = 1 (3)
или
1/t’ - 1/t = 1/f’.
  В тонких Линза (в оптике) t и f можно отсчитывать от соответствующих поверхностей Линза (в оптике)

Из (2) и (3) следует, что по мере приближения изображаемой точки (действительного источника) к фокусу Линза (в оптике) расстояние от изображения до Линза (в оптике) увеличивается; собирающая Линза (в оптике) даёт действительное изображение точки в тех случаях, когда эта точка расположена перед фокусом; если точка расположена между фокусом и Линза (в оптике), её изображение будет мнимым; рассеивающая Линза (в оптике) всегда даёт мнимое изображение действительной светящейся точки (подробнее см. в ст. Изображение оптическое).
 

  Лит.: Элементарный учебник физики, под ред. Г. С. Ландсберга, 6 изд., т. 3, М., 1970; Тудоровский А. И., Теория оптических приборов, 2 изд., т. 1, М. - Линза (в оптике), 1949.
  Г. Г. Слюсарев.