


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Лоренца - Максвелла уравнения
Определение "Лоренца - Максвелла уравнения" в Большой Советской Энциклопедии
Лоренца — Максвелла уравнения, Лоренца уравнения, фундаментальные уравнения классической электродинамики, определяющие микроскопические электромагнитные поля, создаваемые отдельными заряженными частицами. Л. — М. у. лежат в основе электронной теории (микроскопической электродинамики), построенной Х. А. Лоренцом в конце 19 — начале 20 вв. В этой теории вещество (среда) рассматривается как совокупность электрически заряженных частиц (электронов и атомных ядер), движущихся в вакууме.
В Л. — М. у. электромагнитное поле описывается двумя векторами: напряжённостями микроскопических полей — электрического е и магнитного h. Все электрические токи в электронной теории — чисто конвекционные, т. е. обусловлены движением заряженных частиц. Плотность тока j = ru, где r — плотность заряда, а u — его скорость.
Л. — М. у. были получены в результате обобщения макроскопических Максвелла уравнений. В дифференциальной форме в абсолютной системе единиц Гаусса они имеют вид:
rot h = 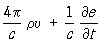 ,
,
rot е = 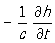 , (1)
, (1)
div h = 0
div е = 4pr
(с — скорость света в вакууме).
Согласно электронной теории, уравнения (1) точно описывают поля в любой точке пространства (в том числе межатомные и внутриатомные поля и даже поля внутри электрона) в любой момент времени. В вакууме они совпадают с уравнениями Максвелла.
Микроскопические напряжённости полей е и h очень быстро меняются в пространстве и времени и непосредственно не приспособлены для описания электромагнитных процессов в системах, содержащих большое число заряженных частиц (то есть в макроскопических материальных телах). А именно такие макроскопические процессы представляют интерес, например, для электротехники и радиотехники. Так, при токе в 1 а через поперечное сечение проводника в 1 сек проходит около 1019 электронов. Проследить за движением всех этих частиц и вычислить создаваемые ими поля невозможно. Поэтому прибегают к статистическим методам, которые позволяют на основе определённых модельных представлений о строении вещества установить связь между средними значениями напряжённостей электрических и магнитных полей и усреднёнными значениями плотностей заряда и тока.
Усреднение микроскопических величин производится по пространственным и временным интервалам, большим по сравнению с микроскопическими интервалами (порядка размеров атомов и времени обращения электронов вокруг ядра), но малым по сравнению с интервалами, на которых макроскопические характеристики электромагнитного поля заметно изменяются (например, по сравнению с длиной электромагнитной волны и её периодом). Подобные интервалы называются «физически бесконечно малыми».
Усреднение Л. — М. у. приводит к уравнениям Максвелла. При этом оказывается, что среднее значение напряжённости микроскопического электрического поля 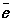 равно напряжённости поля в теории Максвелла:
равно напряжённости поля в теории Максвелла: 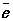 = Е, а среднее значение напряжённости микроскопического магнитного поля
= Е, а среднее значение напряжённости микроскопического магнитного поля 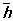 — вектору магнитной индукции:
— вектору магнитной индукции: 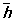 = В.
= В.
В теории Лоренца все заряды разделяются на свободные и связанные (входящие в состав электрически нейтральных атомов и молекул). Можно показать, что плотность связанных зарядов определяется вектором поляризации Р (электрическим дипольным моментом единицы объёма среды):
rсвяз. = - div Р (2)
а плотность тока связанных зарядов, кроме вектора поляризации, зависит также от намагниченности I (магнитного момента единицы объёма среды):
jсвяз. = 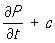 rot I. (3)
rot I. (3)
Векторы Р и I характеризуют электромагнитное состояние среды. Вводя два вспомогательных вектора — вектор электрической индукции
D = E + 4pP (4)
и вектор напряжённости магнитного поля
H = B - 4pI (5)
получают макроскопические уравнения Максвелла для электромагнитного поля в веществе в обычной форме.
Помимо уравнений (1) для микроскопических полей, к основным уравнениям электронной теории следует добавить выражение для силы, действующей на заряженные частицы в электромагнитном поле. Объёмная плотность этой силы (силы Лоренца) равна: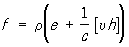 (6)
(6)
Усреднённое значение лоренцовых сил, действующих на составляющие тело заряженные частицы, определяет макроскопическую силу, которая действует на тело в электромагнитном поле.
Электронная теория Лоренца позволила выяснить физический смысл основных постоянных, входящих в уравнения Максвелла и характеризующих электрические и магнитные свойства вещества. На её основе были предсказаны или объяснены некоторые важные электрические и оптические явления (нормальный Зеемана эффект, дисперсия света, свойства металлов и другие).
Законы классической электронной теории перестают выполняться на очень малых пространственно-временных интервалах. В этом случае справедливы законы квантовой теории электромагнитных процессов — квантовой электродинамики. Основой для квантового обобщения теории электромагнитных процессов являются Л. — М. у.
Лит.: Лорентц Г. А., Теория электронов и ее применение к явлениям света и теплового излучения, пер. с английского, 2 издание, М., 1953; Беккер Р., Электронная теория, перевод с немецкого, Л. — М., 1936; Ландау Л. Д. и Лифшиц Е. М., Теория поля, М., 1967 (Теоретическая физика, том 2).
Г. Я. Мякишев.
| "БСЭ" >> "Л" >> "ЛО" >> "ЛОР" |
Статья про "Лоренца - Максвелла уравнения" в Большой Советской Энциклопедии была прочитана 888 раз
| Коптим скумбрию в коробке |
| Куриный суп |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная