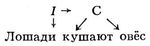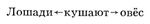Математическая лингвистика

Определение "Математическая лингвистика" в Большой Советской Энциклопедии

Математическая лингвистика. Рис.

Математическая лингвистика, математическая дисциплина, разрабатывающая формальный аппарат для описания строения естественных и некоторых искусственных языков. Возникла в 50-х годах 20 века в связи с назревшей в языкознании потребностью уточнения его основных понятий. В Математическая лингвистика используются по преимуществу идеи и методы алгебры, алгоритмов теории и автоматов теории. Не являясь частью лингвистики, Математическая лингвистика развивается в тесном взаимодействии с ней. Математическая лингвистика называют иногда лингвистические исследования, в которых применяется какой-либо математический аппарат.

Математическая лингвистика. Рис.

Математическое описание языка основано на восходящем к Ф. де Соссюру представлении о языке как механизме, функционирование которого проявляется в речевой деятельности его носителей; её результатом являются «правильные тексты» — последовательности речевых единиц, подчиняющиеся определённым закономерностям, многие из которых допускают математическое описание. Изучение способов математического описания правильных текстов (в первую очередь предложений) составляет содержание одного из разделов Математическая лингвистика — теории способов описания синтаксической структуры. Для описания строения (синтаксической структуры) предложения можно либо выделить в нём «составляющие» — группы слов, функционирующие как цельные синтаксические единицы, либо указать для каждого слова те слова, которые от него непосредственно зависят (если такие есть). Так, в предложении «Лошади кушают овёс» при описании по 1-му способу составляющими будут: всё предложение I, каждое отдельное слово и словосочетание С = «кушают овёс» (рис. 1; стрелки означают «непосредственное вложение»); описание по 2-му способу даёт схему, показанную на рисунке 2. Математические объекты, возникающие при таком описании структуры предложения, называются деревом составляющих (1-й способ) и деревом синтаксического подчинения (2-й способ).

Математическая лингвистика.Рис.

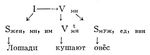
Другой раздел Математическая лингвистика, занимающий в ней центр, место, — теория формальных грамматик, возникшая главным образом благодаря работам Н. Хомского. Она изучает способы описания закономерностей, которые характеризуют уже не отдельный текст, а всю совокупность правильных текстов того или иного языка. Эти закономерности описываются путём построения «формальной грамматики» — абстрактного «механизма», позволяющего с помощью единообразной процедуры получать правильные тексты данного языка вместе с описаниями их структуры. Наиболее широко используемый тип формальной грамматики — так называемая порождающая грамматика, или грамматика Хомского, — упорядоченная система G = <V, W, I, R>, где: V и W — непересекающиеся конечные множества; I — элемент W; R — конечное множество правил вида j®y, где j и y — цепочки (конечные последовательности) элементов V и W. Если j®y правило грамматики G и w ₁, w ₂, — цепочки из элементов V и W, то говорят, что цепочка w ₁yw ₂ непосредственно выводима в G из w ₁jw ₂. Если x₀, x₁, …, x_n — цепочки и для каждого i= 1, ..., n цепочка x_i, непосредственно выводима из x_i-1, то говорят, что x_n выводима из x₀ в G. Множество цепочек из элементов V, выводимых в G из I, называется языком, порождаемым грамматикой G. Если все правила грамматики G имеют вид A®y, где А — элемент W, G называется бесконтекстной, или контекстно-свободной. В лингвистической интерпретации элементы V чаще всего представляют собой слова, элементы W — символы грамматических категорий, I — символ категории «предложение». В бесконтекстной грамматике вывод предложения даёт для него дерево составляющих, в котором каждая составляющая состоит из слов, «происходящих» от одного элемента W, так что для каждой составляющей указывается её грамматическая категория. Так, если грамматика имеет в числе прочих правила I ® S_{x, у, им} V_y, V_y ® V^t_yS_{x, y’ вин}, S_{мyж, ед, вин} ® овёс, S_{жен, мн, им} ® лошади, V^t_мн ® кушают, где V_y означает категорию «группа глагола в числе у», V^t_y — «переходный глагол в числе y», S_x,y,z — «существительное рода х в числе у и падеже z», то приведённое выше предложение имеет вывод, показанный на рис. 3, где стрелки идут из левых частей применяемых правил к элементам соответствующих правых частей. Формальные грамматики используются для описания не только естественных, но и искусственных языков, в особенности языков программирования.

Математическая лингвистика изучает также аналитические модели языка, в которых на основе тех или иных данных о речи, считающихся известными (например, множества правильных предложений), производятся формальные построения, дающие некоторые сведения о структуре языка. Приложение методов Математическая лингвистика к конкретным языкам относится к области лингвистики (см. Языкознание).

  Лит.: Хомский Н., Синтаксические структуры, в сборнике: Новое в лингвистике, в. 2, М., 1962; Гладкий А. В.. Мельчук И. А., Элементы математической лингвистики, М., 1969; Маркус С., Теоретико-множественные модели языков, перевод с английского, М., 1970; Гладкий А. В., Формальные грамматики и языки, М., 1973.
  А. В. Гладкий.