


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Матрица рассеяния
Определение "Матрица рассеяния" в Большой Советской Энциклопедии
Матрица рассеяния, S-maтрица, совокупность величин (матрица), описывающая процесс перехода квантовомеханических систем из одних состояний в другие при их взаимодействии (рассеянии). Понятие «Матрица рассеяния» введено В. Гейзенбергом в 1943.
При рассеянии система переходит из одного квантового состояния, начального (его можно отнести к моменту времени t = —¥) в другое, конечное (t = +¥). Если обозначить набор квантовых чисел, характеризующих начальное состояние, через i, а конечное — через f, то амплитуда рассеяния (квадрат модуля которой определяет вероятность данного рассеяния) может быть записана как Sfi. Совокупность амплитуд рассеяния образует таблицу с двумя входами (i — номер строки, f — номер столбца), которая и называется Матрица рассеяния S. Каждая амплитуда является элементом этой матрицы (матричным элементом). Наборы квантовых чисел i, f могут содержать как непрерывные величины (энергию, угол рассеяния и другие), так и дискретные (орбитальное квантовое число, спин, изотопический спин, массу и т. д.). В простейшем случае системы двух бесспиновых частиц в нерелятивистской квантовой механике состояние определяется относительным импульсом частиц р; тогда амплитуда рассеяния представляет собой функцию двух переменных — энергии Е и угла рассеяния J
Sfi = F (E, J).
В общем случае Матрица рассеяния содержит элементы, отвечающие как упругому рассеянию, так и процессам превращения и рождения частиц. Квадрат модуля матричного элемента ½Sfi½2 определяет вероятность соответствующего процесса (или его эффективное поперечное сечение).
Нахождение Матрица рассеяния — основная задача квантовой механики и квантовой теории поля. Матрица рассеяния содержит всю информацию о поведении системы, если известны не только численные значения, но и аналитические свойства (см. Аналитические функции) её элементов; в частности, её полюсы (см. Особая точка) определяют связанные состояния системы (а следовательно, дискретные уровни энергии). Из основных принципов квантовой теории следует важнейшее свойство Матрица рассеяния — её унитарность. Оно выражается в виде соотношения SS+ = 1 [S+ — матрица, эрмитово сопряжённая S, то есть (S+)fi = S*if, где знак* означает комплексное сопряжение] или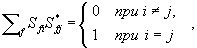
и отражает тот факт, что сумма вероятностей рассеяния по всем возможным каналам реакции должна равняться единице. Соотношение унитарности позволяет устанавливать важные соотношения между различными процессами, а в некоторых случаях даже полностью решить задачу. В релятивистской квантовой механике существует направление, в котором Матрица рассеяния считается первичной динамической величиной; требования унитарности и аналитичности Матрица рассеяния должны служить при этом основой построения полной системы уравнений, определяющей матрицу S.
В. Б. Берестецкий.
| "БСЭ" >> "М" >> "МА" >> "МАТ" >> "МАТР" |
Статья про "Матрица рассеяния" в Большой Советской Энциклопедии была прочитана 943 раз
| Крабы в кокосовом молоке |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная