Многоугольник

Определение "Многоугольник" в Большой Советской Энциклопедии

Многоугольник

Многоугольник, замкнутая ломаная линия. Подробнее, Многоугольник — линия, которая получается, если взять n любых точек A₁, A₂, ..., A_n и соединить прямолинейным отрезком каждую из них с последующей, а последнюю — с первой (см. рис. 1, а). Точки A₁, A₂, ..., A_n называются вершинами Многоугольник, а отрезки A₁A₂, А₂А₃, ..., A_n-1A_n, A_nA₁ — его сторонами. Далее рассматриваются только плоские Многоугольник (т. е. предполагается, что Многоугольник лежит в одной плоскости). Многоугольник может сам себя пересекать (см. рис. 1, б), причём точки самопересечения могут не быть его вершинами.

Многоугольник

Существуют и другие точки зрения на то, что считать Многоугольник Многоугольником можно называть связную часть плоскости, вся граница которой состоит из конечного числа прямолинейных отрезков, называемых сторонами многоугольника. Многоугольник в этом смысле может быть и многосвязной частью плоскости (см. рис. 1, г), т. е. такой Многоугольник может иметь «многоугольные дыры». Рассматриваются также бесконечные Многоугольник — части плоскости, ограниченные конечным числом прямолинейных отрезков и конечным числом полупрямых.

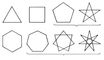
Дальнейшее изложение опирается на данное выше первое определение Многоугольник Если Многоугольник не пересекает сам себя (см., например, рис. 1, а и б), то он разделяет совокупность всех точек плоскости, на нем не лежащих, на две части — конечную (внутреннюю) и бесконечную (внешнюю) в том смысле, что если две точки принадлежат одной из этих частей, то их можно соединить друг с другом ломаной, не пересекающей Многоугольник, а если разным частям, то нельзя. Несмотря на совершенную очевидность этого обстоятельства, строгий его вывод из аксиом геометрии довольно труден (т. н. теорема Жордана для Многоугольник). Внутренняя по отношению к Многоугольник часть плоскости имеет определённую площадь. Если Многоугольник — самопересекающийся, то он разрезает плоскость на определённое число кусков, из которых один бесконечный (называемый внешним по отношению к Многоугольник), а остальные конечные односвязные (называются внутренними), причём граница каждого из них есть некоторый самонепересекающийся Многоугольник, стороны которого есть целые стороны или части сторон, а вершины — вершины или точки самопересечения данного Многоугольник Если каждой стороне Многоугольник приписать направление, т. е. указать, какую из двух определяющих её вершин мы будем считать её началом, а какую — концом, и притом так, чтобы начало каждой стороны было концом предыдущей, то получится замкнутый многоугольный путь, или ориентированный Многоугольник Площадь области, ограниченной самопересекающимся ориентированным Многоугольник, считается положительной, если контур Многоугольник обходит эту область против часовой стрелки, т. е. внутренность Многоугольник остаётся слева от идущего по этому пути, и отрицательной — в противоположном случае. Пусть Многоугольник — самопересекающийся и ориентированный; если из точки, лежащей во внешней по отношению к нему части плоскости, провести прямолинейный отрезок к точке, лежащей внутри одного из внутренних его кусков, и Многоугольник пересекает этот отрезок р раз слева направо и q раз справа налево, то число р — q (целое положительное, отрицательное или нуль) не зависит от выбора внешней точки и называется коэффициентом этого куска. Сумма обычных площадей этих кусков, помноженных на их коэффициенты, считается «площадью» рассматриваемого замкнутого пути (ориентированного Многоугольник). Так определяемая «площадь замкнутого пути» играет большую роль в теории математических приборов (планиметр и др.); она получается там обычно в виде интеграла 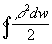 (в полярных координатах r, w) или  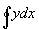(в декартовых координатах х, у), где конец радиус-вектора r или ординаты y один раз обегает этот путь.

Сумма внутренних углов любого самонепересекающегося Многоугольник с n сторонами равна (n — 2)180°. Многоугольник называется выпуклым (см. рис. 1, а), если никакая сторона Многоугольник, будучи неограниченно продолженной, не разрезает Многоугольник на две части. Выпуклый Многоугольник можно охарактеризовать также следующим свойством: прямолинейный отрезок, соединяющий любые две точки плоскости, лежащие внутри Многоугольник, не пересекает Многоугольник Всякий выпуклый Многоугольник — самонепересекающийся, но не наоборот. Например, на рис. 1, б изображен самонепересекающийся Многоугольник, который не является выпуклым, т. к. отрезок PQ, соединяющий некоторые его внутренние точки, пересекает Многоугольник

Важнейшие Многоугольник: треугольники, в частности прямоугольные, равнобедренные, равносторонние (правильные); четырёхугольники, в частности трапеции, параллелограммы, ромбы, прямоугольники, квадраты. Выпуклый Многоугольник называется правильным, если все его стороны равны и все внутренние углы равны. В древности умели по стороне или радиусу описанного круга строить при помощи циркуля и линейки правильные Многоугольник только в том случае, если число сторон Многоугольник равно m = 3 · 2ⁿ, 4 · 2ⁿ,5 · 2ⁿ, 3 · 5 · 2ⁿ, где n — любое положительное число или нуль. Немецкий математик К. Гаусс в 1801 показал, что можно построить при помощи циркуля и линейки правильный Многоугольник, когда число его сторон имеет вид: m = 2ⁿ · p₁ · p₂ · ... · p_k, где p₁, p₂, ... p_k — различные простые числа вида 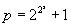 (s — целое положительное число). До сих пор известны только пять таких р: 3, 5, 17, 257, 65537. Из теории Галуа (см. Галуа теория) следует, что никаких других правильных Многоугольник, кроме указанных Гауссом, построить при помощи циркуля и линейки нельзя. Т. о., построение возможно при m = 3, 4, 5, 6, 8, 10, 12, 15 16, 17, 20, 24, 32, 34, ... и невозможно при m = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33, ...

В приведённой ниже таблице указаны радиус описанной окружности, радиус вписанной окружности и площадь правильного n-yгольника (для n = 3, 4, 5, 6, 8, 10), сторона которого равна k.

n	Радиус описанной окружности	Радиус вписанной окружности	Площадь
3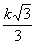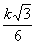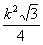
4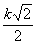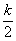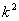
5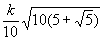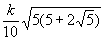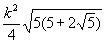
6	k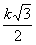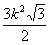
8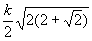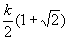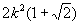
10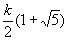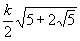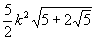

  Начиная с пятиугольника существуют также невыпуклые (самопересекающиеся, или звездчатые) правильные Многоугольник, т. е. такие, у которых все стороны равны и каждая следующая из сторон повёрнута в одном и том же направлении и на один и тот же угол по отношению к предыдущей. Все вершины такого Многоугольник также лежат на одной окружности. Такова, например, пятиконечная звезда. На рис. 2 даны все правильные (как выпуклые, так и невыпуклые) Многоугольник от треугольника до семиугольника.
Лит. см. при ст. Многогранник.