


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Обратная функция
Определение "Обратная функция" в Большой Советской Энциклопедии
Обратная функция, функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) - данная функция, то переменная х, рассматриваемая как функция переменной у, х = j (y), является обратной по отношению к данной функции у = f (x). Например, Обратная функция для у = ax + b (а¹0) является х = (у-b)/a, Обратная функция для у = ех является х = ln у и т.д. Если х = j(y) есть Обратная функция по отношению к у = f (x), то и у = f (x) есть Обратная функция по отношению к х = j(y). Областью определения Обратная функция является область значений данной функции, а областью значений Обратная функция- область определения данной. Графики двух взаимно обратных функций у = f (x) и у = j (x) (где независимое переменное обозначено одной и той же буквой х), как, например, у = ax + b и у = (х-b)/a, у = ех и у = ln х, симметричны по отношению к биссектрисе у = х первого и третьего координатных углов. Функция, обратная по отношению к однозначной функии, может быть многозначной (ср., например, функции х2 и 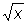 ). Для однозначности Обратная функция необходимо и достаточно, чтобы данная функция у = f (x) принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). Обратная функция по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна.
). Для однозначности Обратная функция необходимо и достаточно, чтобы данная функция у = f (x) принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). Обратная функция по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна.
Если данная функция кусочно монотонна, то, разбивая область её определения на участки её монотонности, получают однозначные ветви Обратная функция Так, одним из участков монотонности для sin х служит интервал - p/2< x < p/2; ему соответствует т. н. главная ветвь arc sin х обратной функции Arc sin х. Для пары однозначных взаимно обратных функций имеют место соотношения j[f (x)]=x и f [j(x)] = х, первое из которых справедливо для всех значений х из области определения функции f (x), а второе - для всех значений х из области определения функции j (x); например, elnx = х (х > 0), 1n (ex) = х (- ¥ < х < ¥). Иногда функцию, обратную к f (x) =у, обозначают f- -1(y) = х, так что для непрерывной и монотонной функции f (x):
F -1[f (x)]=f [f -1) x)]=x.
Вообще же f --1[f (x)] представляет собой многозначную функцию от х, одним из значений которой является х; так, для f (x) = x2, х (¹ 0) является лишь одним из двух значений f --1[f (x)] = √x2 (другое: -х); для f (x) = sin х, х является лишь одним из бесконечного множества значений
f- -1[f (x)] = Arc sin [sin x] = (-1) n x + np,
n = 0, ± 1, ± 2,....
Если у = f (x) непрерывна и монотонна в окрестности точки х = x0 и дифференцируема при х = x0, причём f"(x0) ¹ 0, то f --1(y) дифференцируема при у = у0 и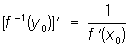
(формула дифференцирования Обратная функция). Так, для -p/2 < х < p/2, у = f (x) = sin х непрерывна и монотонна, f’(x) = cos х ¹ 0 и f- -1(y)= arc sin у (-1< y <1) дифференцируема, причём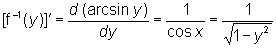
где имеется в виду положительное значение корня (так как cos х > 0 для -p/2 < х < p/2).
| "БСЭ" >> "О" >> "ОБ" >> "ОБР" |
Статья про "Обратная функция" в Большой Советской Энциклопедии была прочитана 731 раз
| Бургер двойного помола |
| Английская картошка фри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная