


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Остроградского формула
Определение "Остроградского формула" в Большой Советской Энциклопедии
Остроградского формула, формула, дающая преобразование интеграла, взятого по объёму Q, ограниченному поверхностью S, в интеграл, взятый по этой поверхности: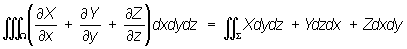 ;
;
здесь X, Y, Z — функции точки (х, у, z), принадлежащей трёхмерной области W. Остроградского формула найдена М. В. Остроградским в 1828 (опубликована в 1831). В векторной форме Остроградского формула имеет вид: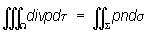 ,
,
где р — вектор поля, заданного в области W; dt — элемент объёма; n — единичный вектор внешней нормали к поверхности S; ds — элемент этой поверхности. В гидродинамическом истолковании Остроградского формула устанавливает равносильность двух способов учёта того количества жидкости, которое вытекает из оболочки S в единицу времени: 1) исходя из «производительности» точечных источников, заполняющих область W (левая часть равенства); 2) исходя из скоростей частиц жидкости в момент их прохождения через оболочку S (правая часть равенства). Формула была дана Остроградским (1834, опубликована в 1838) также и в более общем виде — для интеграла, распространённого на n-мерную область.
| "БСЭ" >> "О" >> "ОС" >> "ОСТ" >> "ОСТР" |
Статья про "Остроградского формула" в Большой Советской Энциклопедии была прочитана 800 раз
| Панайпай |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная