


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Периодическая дробь
Определение "Периодическая дробь" в Большой Советской Энциклопедии
Периодическая дробь, бесконечная десятичная дробь, в которой, начиная с некоторого места, стоит только периодически повторяющаяся определённая группа цифр. Например, 1,3181818...; короче эту дробь записывают так: 1,3(18), то есть помещают период в скобки (и говорят: «18 в периоде»). Периодическая дробь называется чистой, если период начинается сразу после запятой, например 2(71) = 2,7171..., и смешанной, если после запятой имеются цифры, предшествующие периоду, например 1,3(18). Роль Периодическая дробь в арифметике обусловлена тем, что при представлении рациональных чисел, то есть обыкновенных (простых) дробей, десятичными дробями, всегда получаются либо конечные, либо периодические дроби. Точнее: конечная десятичная дробь получается в том случае, когда знаменатель несократимой простой дроби не содержит других простых множителей, кроме 2 и 5; во всех других случаях получается Периодическая дробь, и притом чистая, если знаменатель данной несократимой дроби вовсе не содержит множителей 2 и 5, и смешанная, если хотя бы один из этих множителей содержится в знаменателе. Всякая Периодическая дробь может быть обращена в простую дробь (то есть она равна некоторому рациональному числу). Чистая Периодическая дробь равна простой дроби, числителем которой служит период, а знаменатель изображается цифрой 9, написанной столько раз, сколько цифр в периоде; при обращении в простую дробь смешанной Периодическая дробь числителем служит разность между числом, изображаемым цифрами, предшествующими второму периоду, и числом, изображаемым цифрами, предшествующими первому периоду; для составления знаменателя надо написать цифру 9 столько раз, сколько цифр в периоде, и приписать справа столько нулей, сколько цифр до периода. Эти правила предполагают, что данная Периодическая дробь правильная, то есть не содержит целых единиц; в противном случае целая часть учитывается особо.
Примеры:
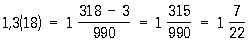
Известны также правила определения длины периода Периодическая дробь, соответствующей данной обыкновенной дроби. Например, для дроби a/p, где р — простое число и 1 £ a £ p — 1, длина периода является делителем р — 1. Так, для известных приближений к числу (см. Пи) 22/7 и 355/113 период равен 6 и 112 соответственно.
| "БСЭ" >> "П" >> "ПЕ" >> "ПЕР" >> "ПЕРИ" |
Статья про "Периодическая дробь" в Большой Советской Энциклопедии была прочитана 1100 раз
| Бургер двойного помола |
| Английская картошка фри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная