Повторного логарифма закон

Значение слова "Повторного логарифма закон" в Большой Советской Энциклопедии

Повторного логарифма закон, одна из предельных теорем теории вероятностей, близкая по смыслу к закону больших чисел (см. Больших чисел закон). Повторного логарифма закон указывает при определённых условиях точный порядок роста сумм независимых случайных величин при увеличении числа слагаемых. Пусть, например, случайные величины X₁, X₂,..., X_n,... независимы и каждая из них принимает два значения: +1 или —1, каждое с вероятностью, равной ¹/₂, и пусть s_n= X₁ +... + X_n. Тогда с вероятностью, равной 1, при любом d > 0:

1) при всех n, больших некоторого (зависящего от случая) номера N:

s_n < (1 + d)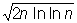

2) для бесконечной последовательности номеров n:

s_n > (1 - d)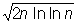

.

Название «Повторного логарифма закон» объясняется наличием в вышеприведённых выражениях множителя In In n. Повторного логарифма закон возник из задач т. н. метрической теории чисел (см. Чисел теория). Первый результат, относящийся к Повторного логарифма закон, был установлен в 1924 А. Я. Хинчиным. Дальнейшие существенные продвижения в изучении условий приложимости Повторного логарифма закон связаны с работами А. Н. Колмогорова (1929) и В. Феллера (1943).

Лит.: Феллер В., Введение в теорию вероятностей и её приложения, пер. с англ., 2 изд., т. 1, М., 1967.

Ю. В. Прохоров.

В Большой Советской Энциклопедии рядом со словом "Повторного логарифма закон"

Повторитель | Буква "П" | В начало | Буквосочетание "ПО" | Повторные посевы

Статья про слово "Повторного логарифма закон" в Большой Советской Энциклопедии была прочитана 0 раз

Интересное

Florists in america

business support in USA