


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Почти периодическая функция
Определение "Почти периодическая функция" в Большой Советской Энциклопедии
Почти периодическая функция, функция, значения которой при добавлении к аргументу надлежащим образом выбранных постоянных чисел (почти периодов) приближённо повторяются. Более точно: непрерывная функция f (x), определённая для всех действительных значений х, называется почти периодической, если для каждого e > 0 можно указать такое l = l (e), что в каждом интервале оси х длины l найдётся хотя бы одно число t = t(e), для которого при любом х выполняется неравенство |f (x + t) — f (x)| < e. Числа t называются почти периодами функции f (x). Периодическая функции суть частные случаи Почти периодическая функция; простейшие примеры Почти периодическая функция, не являющихся периодическими, получаются в результате сложения периодических функций с несоизмеримыми периодами, например cosx + cos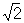 x.
x.
Некоторые наиболее важные свойства Почти периодическая функция:
1) Почти периодическая функция ограничена и равномерно непрерывна на всей оси х.
2) Сумма и произведение конечного числа Почти периодическая функция есть также Почти периодическая функция
3) Предел равномерно сходящейся последовательности Почти периодическая функция есть также Почти периодическая функция
4) Для каждой Почти периодическая функция существует среднее значение (на всей оси х):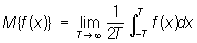 .
.
5) Каждой Почти периодическая функция можно сопоставить ряд Фурье: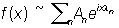 ,
,
причём l1, l2, …, ln, …, может быть любой последовательностью отличных друг от друга действительных чисел и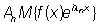 .
.
6) Равенство Парсеваля: для каждой Почти периодическая функция справедливо равенство:
M {|f (x)|2} = 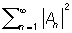 .
.
7) Теорема единственности: если f (x) есть непрерывная Почти периодическая функция и если для всех действительных l
М {f (х) е-ilx} = 0,
то f (x) º 0. Иначе говоря, ряд Фурье однозначно определяет Почти периодическая функция
8) Теорема аппроксимации: для каждого e > 0 можно указать такой конечный тригонометрический полином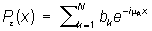
(mk — действительные числа), что для всех значений х выполняется неравенство: |f (x) — Pe(x)| < e; обратно, каждая функция f (x) с этим свойством является Почти периодическая функция
Первое построение непрерывных Почти периодическая функция было дано датским математиком Х. Бором (1923). Ещё ранее (1893) частный случай Почти периодическая функция — т. н. квазипериодические функции — изучил латвийский математик П. Боль. Новое построение теории Почти периодическая функция дал Н. Н. Боголюбов (1930). Обобщение теории Почти периодическая функция на разрывные функции впервые дано В. В. Степановым (1925), а потом Г. Вейлем и А. Безиковичем. Обобщение другого рода было дано советским математиком Б. М. Левитаном (1938).
Лит.: Бор Г., Почти периодические функции, пер. с нем., М. — Л., 1934; Левитан Б. М., Почти-периодические функции, М., 1953.
| "БСЭ" >> "П" >> "ПО" >> "ПОЧ" |
Статья про "Почти периодическая функция" в Большой Советской Энциклопедии была прочитана 1241 раз
| Бургер двойного помола |
| Крабы в кокосовом молоке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная