


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Приближённые формулы
Определение "Приближённые формулы" в Большой Советской Энциклопедии
Приближённые формулы, математические формулы, получаемые из формул вида f (x) = f*(x) + e(х), где e(х) рассматривается как погрешность и после оценки отбрасывается. Таким образом, Приближённые формулы имеет вид f (x) » f*(x).
Например, Приближённые формулы (1 + х)2 » 1 + 2x получается из точной формулы для (1 + х)2 при малых |x|; этой формулой можно пользоваться при вычислении с точностью до сотых, тысячных, десятитысячных, если |x| соответственно не больше 0,0707..., 0,0223..., 0,00707... Эта Приближённые формулы даёт результат тем более точный, чем х ближе к 0. Но так бывает не всегда. Например, точность Приближённые формулы tg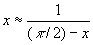 тем больше, чем х ближе к p/2.
тем больше, чем х ближе к p/2.
Выше (стр. 555) приведено несколько наиболее употребительных Приближённые формулы, причём показано, какого числа не должно превосходить |x|, чтобы формула давала k точных десятичных знаков.
Часто Приближённые формулы получают с помощью разложения функций в ряды, например в ряд Тейлора. Чтобы уверенно применять Приближённые формулы, необходимо иметь оценку разности между точным и приближённым выражениями функции. Зная, например, что разность между sinx и двучленом 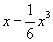 не превосходит по абсолютному значению
не превосходит по абсолютному значению 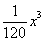 , легко убедиться, что Приближённые формулы
, легко убедиться, что Приближённые формулы 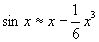 даёт значения sinx с точностью до сотых, тысячных, десятитысячных, если х соответственно меньше 0,89 (51°), 0,55 (32°), 0,34 (20°).
даёт значения sinx с точностью до сотых, тысячных, десятитысячных, если х соответственно меньше 0,89 (51°), 0,55 (32°), 0,34 (20°).
| "БСЭ" >> "П" >> "ПР" >> "ПРИ" >> "ПРИБ" |
Статья про "Приближённые формулы" в Большой Советской Энциклопедии была прочитана 523 раз
| Бургер двойного помола |
| Стейк на сливочном масле |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная