


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Пропорциональность
Определение "Пропорциональность" в Большой Советской Энциклопедии
Пропорциональность, простейший вид функциональной зависимости (см. Функция). Различают прямую и обратную Пропорциональность Две переменные величины называют прямо пропорциональными (или просто пропорциональными), если отношение их не изменяется, т. е. во сколько раз увеличится (или уменьшится) одна из них, во столько же раз увеличится (или уменьшится) и другая. Аналитически Пропорциональность величин х и у характеризуется соотношением: у = kx, где k - т. н. коэффициент пропорциональности. Графически пропорциональная зависимость изображается прямой линией (или полупрямой), проходящей через начало координат, угловой коэффициент которой равен коэффициенту Пропорциональность Переменные величины х и у называют обратно пропорциональными, если одна из них пропорциональна обратному значению другой, т. е. у = 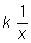 или ху = k. Графиком обратно пропорциональной зависимости служит равнобочная гипербола (или одна её ветвь). Пропорциональная зависимость встречается чрезвычайно часто. Примеры: путь S, пройденный телом при равномерном движении, пропорционален времени t (S = kt, k - скорость); вес Р однородного тела пропорционален его объёму v (P = ku, k - удельный вес); время выемки данного количества грунта обратно пропорционально производительности труда и т.п.
или ху = k. Графиком обратно пропорциональной зависимости служит равнобочная гипербола (или одна её ветвь). Пропорциональная зависимость встречается чрезвычайно часто. Примеры: путь S, пройденный телом при равномерном движении, пропорционален времени t (S = kt, k - скорость); вес Р однородного тела пропорционален его объёму v (P = ku, k - удельный вес); время выемки данного количества грунта обратно пропорционально производительности труда и т.п.
| "БСЭ" >> "П" >> "ПР" >> "ПРО" >> "ПРОП" |
Статья про "Пропорциональность" в Большой Советской Энциклопедии была прочитана 549 раз
| Пицца в сковороде |
| Кишки на гриле |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная