Библиотека DJVU
БСЭ
Статистика:
Пуассона формула суммирования
Значение слова "Пуассона формула суммирования" в Большой Советской Энциклопедии
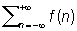
Если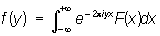
- Фурье преобразование (несколько иначе, чем обычно, нормированное) функции F (x), то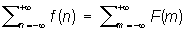
(m и n - целые). Это и есть Пуассона формула суммирования; она может быть записана в более общем виде: если l > 0, m > 0, lm = 1 и 0 £ t < 1, то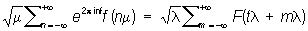
Для справедливости этой формулы достаточно, чтобы в каждом конечном интервале F (x) имела ограниченную вариацию, и для х ® + ¥ и х ® - ¥ выполнялось одно из условий: 1) F (x) - монотонна и абсолютно интегрируема; 2) F (x) - интегрируема и обладает абсолютно интегрируемой производной. Пуассона формула суммирования позволяет в ряде случаев заменить вычисление суммы ряда вычислением суммы др. ряда, сходящегося быстрее первоначального.
В Большой Советской Энциклопедии рядом со словом "Пуассона формула суммирования"
Пуассона уравнение | Буква "П" | В начало | Буквосочетание "ПУ" | Пуассоновский потокСтатья про слово "Пуассона формула суммирования" в Большой Советской Энциклопедии была прочитана 0 раз
Интересное