


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Равенство (математич.)
Определение "Равенство (математич.)" в Большой Советской Энциклопедии
Равенство, отношение взаимной заменимости (подстановочности) объектов, которые именно в силу их взаимной заменимости считают равными. Такое понимание Равенство (математич.) восходит к Г. В. Лейбницу. Взаимозаменимость может быть более или менее полной, что связано с глубиной (или интервалом) Равенство (математич.), но, вообще говоря, она всегда относительна, поскольку приравниваемые объекты — будь то предметы объективного мира или наши мысли (идеи, понятия, высказывания и пр.) — индивидуальны и неповторимы: в понятии «взаимозаменимые объекты» уже содержится посылка о разделяющем их условии (признаке), т. е. индивидуация. Степень полноты взаимозаменимости (размерность Равенство (математич.)) естественно возрастает от сходства к тождеству. В последнем случае говорят просто о неразличимости, которую обычно приводят как критерий логического Равенство (математич.) (тождества), что, однако, неточно, поскольку неразличимость гарантирует, вообще говоря, только Равенство (математич.) в интервале (с точностью до) условий неразличимости, а это последнее, в отличие от логического Равенство (математич.), не связано с обязательным выполнением транзитивности. Тем не менее стало уже традицией говорить о принципе Равенство (математич.) неразличимых, который в языке логики предикатов первого порядка выражается аксиомой (экстенсиональности):
х = у É (j(x) É (у))
и аксиомой х = х, а в языке второго порядка определением: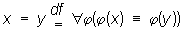 .
.
Практикуемая в приложениях логики замена этих выражений конечным списком «содержательных» аксиом Равенство (математич.) для всех исходных индивидуальных функций и предикатов рассматриваемой теории с добавлением аксиом рефлексивности (х = х), симметричности (х = у É у = х) и транзитивности (х = y&y = z É x = z) Равенство (математич.) является по существу переходом от чисто логической формулировки Равенство (математич.) к более слабой его формулировке — к Равенство (математич.) в интервале абстракции отождествления по предикатам конкретной Тождество).
Лит.: Шрейдер Ю. Равенство, сходство, порядок, М., 1971; Математическая логика, пер. с англ., М., 1973, с. 181—199.
М. М. Новосёлов.
| "БСЭ" >> "Р" >> "РА" >> "РАВ" |
Статья про "Равенство (математич.)" в Большой Советской Энциклопедии была прочитана 740 раз
| Бургер двойного помола |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная