


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Симпсона формула
Определение "Симпсона формула" в Большой Советской Энциклопедии
Симпсона формула, формула для приближённого вычисления определённых интегралов, имеющая вид: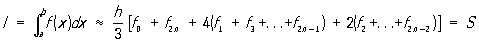 ,
,
где h = (b - а)/2n; fi, = f (a + ih), i = 0, 1, 2,..., 2n. Симпсона формула называют иногда формулой парабол, т. к. вывод этой формулы основан на замене подынтегральной функции f (x) на каждом из отрезков [a + 2hk, а + 2h (k + 1)], k = 0, 1,..., n - 1, соответствующим интерполяционным многочленом второй степени (см. Интерполяционные формулы); геометрически это означает, что кривая, описываемая уравнением у = f (x), заменяется близкой к ней кривой, состоящей из отрезков парабол. Погрешность, возникающая в результате применения Симпсона формула, равна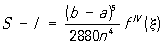 ,
,
где а £ x £ b. Если подынтегральная функция f (x) - многочлен степени m £ 3, то Симпсона формула является не приближённой, а точной, так как в этом случае f IV (x) º 0.
Симпсона формула названа по имени Т. Симпсона, получившего её в 1743, хотя эта формула была известна ранее, например Дж. Грегори (1668).
О других формулах для приближённого вычисления определённых интегралов см. в ст. Приближённое интегрирование.
| "БСЭ" >> "С" >> "СИ" >> "СИМ" >> "СИМП" |
Статья про "Симпсона формула" в Большой Советской Энциклопедии была прочитана 668 раз
| Пицца в сковороде |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Объединённая партия гаитянских коммунистов
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная