


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Сингулярные интегральные уравнения
Определение "Сингулярные интегральные уравнения" в Большой Советской Энциклопедии
Сингулярные интегральные уравнения, интегральные уравнения с ядрами, обращающимися в бесконечность в области интегрирования так, что соответствующий несобственный интеграл, содержащий неизвестную функцию, расходится и заменяется своим главным значением по Коши. Примером Сингулярные интегральные уравнения может служить следующее уравнение с т. н. ядром Гильберта: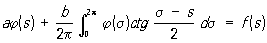
решением которого является функция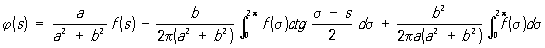 ,
,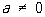 ,
, 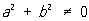 ,
,
где первый интеграл также понимается в смысле главного значения по Коши.
Хорошо изученным общим классом Сингулярные интегральные уравнения являются уравнения с ядром Коши вида: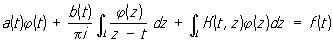 , (*)
, (*)
где a (t), b (t), f (t) - заданные непрерывные функции точки t пути интегрирования L (который может состоять из конечного числа гладких самонепересекающихся замкнутых или незамкнутых кривых с непрерывной кривизной) в комплексной плоскости; сингулярный интеграл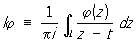
понимается как предел при e ® 0 интеграла 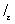 j по пути Le, который получается из L после удаления симметричной относительно точки t дуги длины 2e. Ядро K (t, z) предполагается принадлежащим к одному из тех классов, которые рассматриваются в теории несингулярных интегральных уравнений. К Сингулярные интегральные уравнения вида (*) приводят многие задачи теории аналитических функций, теории упругости, гидродинамики и др.
j по пути Le, который получается из L после удаления симметричной относительно точки t дуги длины 2e. Ядро K (t, z) предполагается принадлежащим к одному из тех классов, которые рассматриваются в теории несингулярных интегральных уравнений. К Сингулярные интегральные уравнения вида (*) приводят многие задачи теории аналитических функций, теории упругости, гидродинамики и др.
Исследование Сингулярные интегральные уравнения (*) опирается на свойства сингулярного интеграла Ij, которые зависят от предположений, делаемых относительно j. Подробно Сингулярные интегральные уравнения исследованы в пространстве непрерывных функций j и в пространстве функций, интегрируемых с квадратом. Основное свойство сингулярного интеграла Ij выражается равенством 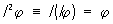 , справедливым для широкого класса функций.
, справедливым для широкого класса функций.
Многие результаты теории Сингулярные интегральные уравнения почти без изменений переносятся на системы Сингулярные интегральные уравнения, которые можно записать в виде (*), если под а и b понимать матричные функции, а под f и j - векторы (одноколонные матрицы). Теория обобщается также на случай системы Сингулярные интегральные уравнения с разрывными коэффициентами и кусочно-гладким путём интегрирования. Изучены также некоторые классы Сингулярные интегральные уравнения в многомерных областях.
Сингулярные интегральные уравнения впервые (начало 20 в.) встретились в исследованиях А. Пуанкаре (по теории приливов) и Д. Гильберта (по краевым задачам). Ряд важных свойств Сингулярные интегральные уравнения установил нем. математик Ф. Нётер. Для разработки теории Сингулярные интегральные уравнения важное значение имели работы Т. Карлемана и И. И. Привалова. Наиболее полные результаты получены сов. учёными (Н. И. Мусхелишвили, И. Н. Векуа, В. Д. Купрадзе и др.).
Лит.: Мусхелишвили Н. И., Сингулярные интегральные уравнения. Граничные задачи теории функций и некоторые их приложения к математической физике, 3 изд., М., 1968; Векуа Н. П., Системы сингулярных интегральных уравнений и некоторые граничные задачи, 2 изд., М., 1970.
| "БСЭ" >> "С" >> "СИ" >> "СИН" >> "СИНГ" |
Статья про "Сингулярные интегральные уравнения" в Большой Советской Энциклопедии была прочитана 517 раз
| Коптим скумбрию в коробке |
| Гороховое пюре |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная