


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Сложная функция
Определение "Сложная функция" в Большой Советской Энциклопедии
Сложная функция, функция от функции. Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то есть u = j(х), то у является Сложная функция от х, то есть y = f [(x)], определённой для тех значений х, для которых значения j(х) входят в множество определения функции f (u). В таком случае говорят, что у является Сложная функция независимого аргумента х, а u - промежуточным аргументом. Например, если у = u2, u = sinx, то у = sin2х для всех значений х. Если же, например, у = 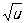 , u = sinx, то у =
, u = sinx, то у = 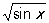 , причём, если ограничиваться действительными значениями функции, Сложная функция у как функция х определена только для таких значений х, для которых sin ³ 0, то есть для
, причём, если ограничиваться действительными значениями функции, Сложная функция у как функция х определена только для таких значений х, для которых sin ³ 0, то есть для 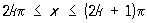 , где k = 0, ± 1, ± 2,...
, где k = 0, ± 1, ± 2,...
Производная Сложная функция равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимому аргументу. Это правило (цепное правило) распространяется на Сложная функция с двумя, тремя и т. д. промежуточными аргументами: если у = f (u1), u1 = j(u2),..., uk-1 = jk-1(uk), uk = jk (x), то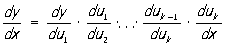
| "БСЭ" >> "С" >> "СЛ" >> "СЛО" |
Статья про "Сложная функция" в Большой Советской Энциклопедии была прочитана 647 раз
| Бургер двойного помола |
| Крабы в кокосовом молоке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная