


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Стокса проблема
Определение "Стокса проблема" в Большой Советской Энциклопедии
Стокса проблема, задача об определении внешнего гравитационного поля планеты по её внешней уровенной поверхности S, массе внутри S и угловой скорости вращения около некоторой оси. Дж. Г. Стокс доказал разрешимость этой задачи и дал приближённое решение для сжатого сфероида с относительной ошибкой порядка квадрата его сжатия как первой краевой задачи теории потенциала. Точное решение Стокса проблема для эллипсоида получено итальянским учёным П. Пиццетти и М. С. Молоденским. Произвольной форме S соответствуют краевое условие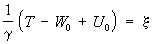
и уравнение относительно j: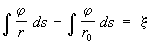
При условии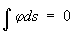
где x — высота S над отсчётным эллипсоидом S0, содержащим заданную массу; возмущающий потенциал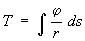
j — плотность простого слоя на S, W0 — потенциал силы тяжести в начале счёта x на пересечении S и S0, U0 — то же на S0, g— сила. тяжести в поле эллипсоида, r — расстояние между элементом ds и точкой на S с высотой x, r0 — то же между ds и точкой, являющейся началом счёта x. Оси вращения S и S0 совпадают. Уравнение для j можно заменить системой линейных алгебраических уравнений. Определение j решает задачу, именуемую Стокса проблема Изложенное решение пригодно и в том случае, когда S — неуровенная и t, — высота квазигеоида (см. Геоид).
Лит.: Молоденскиqй М. С., Еремеев В. Ф., Юркина М. И., Методы изучения внешнего гравитационного поля и фигуры Земли, М., 1960 (Тр. Центр, н.-и. института геодезии, аэросъемки и картографии, в. 131): Stokes G. G., On attractions and on Clairaut"s theorem, «Cambridge and Dublin mathematical journal», 1849, v. 4.
М. И. Юркина.
| "БСЭ" >> "С" >> "СТ" >> "СТО" >> "СТОК" |
Статья про "Стокса проблема" в Большой Советской Энциклопедии была прочитана 499 раз
| Бургер двойного помола |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная