


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Тейлора формула
Определение "Тейлора формула" в Большой Советской Энциклопедии
Тейлора формула, формула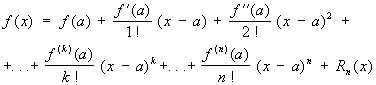
изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n [то есть Rn (x) = an (x)(x—a) n, где an (x) ® 0 при х ® а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x) можно представить в видах: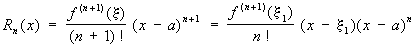 ,
,
где x и x1 — какие-то точки указанного интервала (остаточный член Тейлора формула в формах Лагранжа и соответственно Коши). График многочлена, входящего в Тейлора формула. имеет в точке а соприкосновение не ниже n-го порядка с графиком функции f (x). Тейлора формула применяют для исследования функций и для приближённых вычислений.
Лит.: Хинчин А. Я., Краткий курс математического анализа, М.. 1953; Фихтенгольц Г. М.. Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М.. 1969.
| "БСЭ" >> "Т" >> "ТЕ" >> "ТЕЙ" |
Статья про "Тейлора формула" в Большой Советской Энциклопедии была прочитана 720 раз
| Бургер двойного помола |
| Кимчи из грибов |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная