Бернулли уравнение (гидродинамики)

Определение "Бернулли уравнение (гидродинамики)" в Большой Советской Энциклопедии

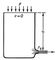Истечение из открытого сосуда

Бернулли уравнение, основное уравнение гидродинамики, связывающее (для установившегося течения) скорость текущей жидкости v, давление в ней р и высоту h расположения малого объёма жидкости над плоскостью отсчёта. Бернулли уравнение (гидродинамики) было выведено Д. Бернулли в 1738 для струйки идеальной несжимаемой жидкости постоянной плотности r, находящейся под действием только сил тяжести. В этом случае Бернулли уравнение (гидродинамики) имеет вид:
v²/2 + plr + gh = const,

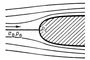Обтекание препятствия

где g - ускорение силы тяжести. Если это уравнение умножить на r, то 1-й член будет представлять собой кинетическую энергию единицы объёма жидкости, а др. 2 члена - его потенциальную энергию, часть которой обусловлена силой тяжести (последний член уравнения), а др. часть - давлением p. Бернулли уравнение (гидродинамики) в такой форме выражает закон сохранения энергии. Если вдоль струйки жидкости энергия одного вида, например кинетическая, увеличивается, то потенциальная энергия на столько же уменьшается. Поэтому, например, при сужении потока, текущего по трубопроводу, когда скорость потока увеличивается (т.к. через меньшее сечение за то же время проходит такое же количество жидкости, как и через большее сечение), давление соответственно в нём уменьшается (на этом основан принцип работы расходомера Вентури).

Из Бернулли уравнение (гидродинамики) вытекает ряд важных следствий. Например, при истечении жидкости из открытого сосуда под действием силы тяжести (рис. 1) из Бернулли уравнение (гидродинамики) следует:
v²/2g = h   или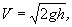

т. е. скорость жидкости в выходном отверстии такова же, как при свободном падении частиц жидкости с высоты h.

Если равномерный поток жидкости, скорость которого v₀ и давление p₀, встречает на своём пути препятствие (рис. 2), то непосредственно перед препятствием происходит подпор - замедление потока; в центре области подпора, в критической точке, скорость потока равна нулю. Из Бернулли уравнение (гидродинамики) следует, что давление в критической точке p₁ = p₀ + rv²₀/2. Приращение давления в этой точке, равное p₁ - p₀ = rv²₀/2, называется динамическим давлением, или скоростным напором. В струйке реальной жидкости её механическая энергия не сохраняется вдоль потока, а расходуется на работу сил трения и рассеивается в виде тепловой энергии, поэтому при применении Бернулли уравнение (гидродинамики) к реальной жидкости необходимо учитывать потери на сопротивление.

Бернулли уравнение (гидродинамики) имеет большое значение в гидравлике и технической гидродинамике: оно используется при расчётах трубопроводов, насосов, при решении вопросов, связанных с фильтрацией, и т.д. Бернулли уравнение для среды с переменной плотностью р вместе с уравнением неизменяемости массы и уравнением состояния является основой газовой динамики.
  Лит.: Фабрикант Н.Я., Аэродинамика, ч. 1-2, Л.,1949- 64; Угинчус А. А., Гидравлика, гидравлические машины и основы сельскохозяйственного водоснабжения, К.-М., 1957, гл. V.