


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Факторный анализ
Определение "Факторный анализ" в Большой Советской Энциклопедии
Факторный анализ, раздел статистического анализа многомерного,. объединяющий методы оценки размерности множества наблюдаемых переменных посредством исследования структуры ковариационных или корреляционных матриц. Основное предположение Факторный анализ заключается в том, что корреляционные связи между большим числом наблюдаемых переменных определяются существованием меньшего числа гипотетических ненаблюдаемых переменных или факторов. В терминах случайных величин – результатов наблюдений X1,..., Xn общей моделью Факторный анализ служит следующая линейная модель: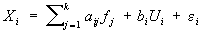 (*),
(*),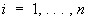 ,
,
где случайные величины fj суть общие факторы, случайные величины Ui суть факторы, специфические для величин Xi и не коррелированные с fj, а ei; суть случайные ошибки. Предполагается, что k < n задано, случайные величины ei независимы между собой и с величинами fj и Ui и имеют Еei = 0, Dei = s2i. Постоянные коэффициенты aij называются факторными нагрузками (нагрузка i-й переменной на j-й фактор). Значения aij, bi, и s2i считаются неизвестными параметрами, подлежащими оценке. В указанной форме модель Факторный анализ отличается некоторой неопределённостью, т.к. n переменных выражаются здесь через n + k других переменных. Однако уравнения (*) заключают в себе гипотезу о ковариационной матрице, которую можно проверить. Например, если факторы fj некоррелированы и cij – элементы матрицы ковариаций между величинами Xi, то из уравнений (*) следует выражение для cij через факторные нагрузки и дисперсии ошибок: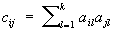 ,
, 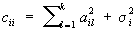 .
.
Т. о., общая модель Факторный анализ равносильна гипотезе о ковариационной матрице, а именно о том, что ковариационная матрица представляется в виде суммы матрицы А = {aij} и диагональной матрицы L с 2 элементами s2i.
Процедура оценивания в Факторный анализ состоит из двух этапов: оценки факторной структуры – числа факторов, необходимого для объяснения корреляционной связи между величинами Xi, и факторной нагрузки, а затем оценки самих факторов по результатам наблюдения. Принципиальные трудности при интерпретации набора факторов состоят в том, что при k > 1 ни факторные нагрузки, ни сами факторы не определяются однозначно, т.к. в уравнении (*) факторы fj могут быть заменены любым ортогональным преобразованием. Это свойство модели используется в целях преобразования (вращения) факторов, которое выбирается так, чтобы наблюдаемые величины имели бы максимально возможные нагрузки на один фактор и минимальные нагрузки на остальные факторы. Существуют различные практические способы оценки факторных нагрузок, имеющие смысл в предположении, что Xi,..., Xn подчиняются многомерному нормальному распределению с ковариационной матрицей С = {сij}. Выделяется максимального правдоподобия метод, который приводит к единственным оценкам для cij, но для оценок aij даёт уравнения, которым удовлетворяет бесчисленное множество решений, одинаково хороших по статистическим свойствам.
Факторный анализ возник и первоначально разрабатывался в задачах психологии (1904). Область его приложения значительно шире – Факторный анализ находит применение при решении различных практических задач в медицине, экономике, химии и т.д. Однако многие результаты и методы Факторный анализ пока ещё не обоснованы, хотя практики ими широко пользуются. Математическое строгое описание современного Факторный анализ – задача весьма трудная и до сих пор в полной мере не решенная.
Лит.: Лоул и Д., Максвелл А., Факторный анализ как статистический метод, пер. с англ., М., 1967; Харман Г., Современный факторный анализ, пер. с англ., М., 1972.
А. В. Прохоров.
| "БСЭ" >> "Ф" >> "ФА" >> "ФАК" |
Статья про "Факторный анализ" в Большой Советской Энциклопедии была прочитана 809 раз
| Бургер двойного помола |
| Английский рыбный пирог |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная