Геодезия

Определение "Геодезия" в Большой Советской Энциклопедии

Геодезический сигнал

Геодезия (греч. geōdaisía, от gē — Земля и dáiō — делю, разделяю), наука об определении фигуры, размеров и гравитационного поля Земли и об измерениях на земной поверхности для отображения её на планах и картах, а также для проведения различных инженерных и народно-хозяйственных мероприятий. Название «геодезия» («землеразделение») указывает на те первоначальные практические задачи, которые обусловили её возникновение, но не раскрывает её современных научных проблем и практических задач, связанных с разнообразными потребностями человеческой деятельности.

Монумент на южном конце дуги меридиана Струве (Старо-Некрасовка, близ Измаила)

Основные задачи геодезии. При определении фигуры и размеров Земли в Геодезия исходят из понятия об уровенных поверхностях Земли, т. е. о таких поверхностях, на каждой из которых потенциал силы тяжести имеет всюду соответствующее постоянное значение и которые пересекают направления отвесной линии под прямым углом. Направление отвесной линии в Геодезия принимают за одну из координатных линий, т. к. оно в каждой данной точке может быть построено однозначно при помощи уровня или даже простейшего отвеса.

Нивелирный репер

Поверхность воды в океанах и сообщающихся с ними морях в состоянии полного покоя и равновесия являлась бы одной из уровенных поверхностей Земли. Эту уровенную поверхность, мысленно продолженную под материками так, чтобы она везде пересекала направление отвесной линии под прямым углом, в Геодезия принимают за основную уровенную поверхность Земли (рис. 1). Фигуру же этой уровенной поверхности в Геодезия принимают за сглаженную фигуру Земли и называют геоидом.

Подземный центр геодезического пункта (разрез)

  Теория фигуры Земли и результаты астрономических и геодезических измерений показывают, что фигура геоида в общем близка к эллипсоиду вращения. Эллипсоид, который по своим размерам и положению в теле Земли наиболее правильно представляет фигуру геоида в целом, называют общим земным эллипсоидом. Изучение фигуры Земли заключается в определении размеров земного эллипсоида и его положения в теле самой Земли, а также отступлений геоида от этого эллипсоида. Если определить высоты точек земной поверхности относительно геоида, т. е. над уровнем моря, то тем самым будет изучена и фигура физической поверхности Земли, Размеры земного эллипсоида и его положение в теле Земли устанавливают путём определения направлений отвесных линий в избранных точках земной поверхности и взаимного положения этих точек в известной системе координат. Направление отвесной линии в данной точке характеризуется её астрономической широтой и долготой, которые выводятся из астрономических наблюдений. Взаимное положение точек земной поверхности определяется их геодезическими широтами и долготами (см. Геодезические координаты), которые характеризуют направления нормалей в этих точках к поверхности т. н. референц-эллипсоида. Угол между отвесной линией и нормалью к поверхности референц-эллипсоида в данной точке есть отклонение отвеса и характеризует наклон уровенной поверхности Земли относительно поверхности референц-эллипсоида в этой точке. По наблюдённым отклонениям отвеса в избранных точках определяют как размеры земного эллипсоида, так и высоты геоида (см. Астрономо-гравиметрическое нивелирование), Совокупность астрономических и геодезических измерений, позволяющих определять фигуру и размеры Земли, носит название градусных измерений и приводит к геометрическим методам решения этой проблемы. Существуют и физические, или динамические, методы изучения фигуры и гравитационного поля Земли. Они основаны на измерениях ускорения силы тяжести и наблюдениях за движением искусственных спутников Земли и космических летательных аппаратов. Измеренные величины силы тяжести сравнивают с соответствующими теоретическими величинами, рассчитанными для известной эллипсоидальной уровенной поверхности. Разности тех и других величин силы тяжести называют аномалиями силы тяжести и характеризуют отклонения уровенных поверхностей Земли от поверхности эллипсоида. Они позволяют определить сжатие Земли и отступления геоида от земного эллипсоида. Отступление реальной фигуры Земли от правильной шарообразной формы и аномалии гравитационного поля Земли вызывают возмущения орбит искусственных космических объектов. Зная же возмущения орбит искусственных космических тел, на основании наблюдений и измерений можно определить фигуру и внешнее гравитационное поле Земли. совместно применение геометрических и динамических методов позволяет определить одновременно фигуру, размеры и гравитационное поле Земли как планеты.

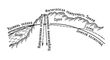Разрез земной поверхности вертикальной плоскостью

Отклонения отвеса и аномалии силы тяжести отражают особенности внутреннего строения Земли и используются для выяснения вопросов о распределении масс внутри Земли и особенно для изучения строения земной коры. Данные о фигуре, размерах и гравитационном поле Земли имеют большое значение для установления масштаба взаимных расстояний и масс небесных тел. Они используются также для механико-математических расчётов, связанных с запуском космических летательных аппаратов и с изучением космического пространства вообще. Другие задачи Геодезия состоят в различных измерениях на земной поверхности для отображения её на планах и топографических картах, которые имеют большое значение для военного дела и без которых не обходится ни одно народно-хозяйственное и инженерно-техническое мероприятие. Геодезические работы производятся с целью изыскания, проектирования и строительства гидротехнических сооружений и промышленных предприятий, ирригационных и судоходных каналов, наземных и подземных путей сообщения и т. п. Геодезические работы и топографические карты служат основой планировки городов и населённых пунктов, землеустроительных и лесоустроительных мероприятий, поиска полезных ископаемых и освоения природных богатств и т. д. Иногда приходится считаться с тем, что фигура и гравитационное поле Земли, а также земная поверхность претерпевают изменения, обусловленные различными внешними и внутренними причинами. Эти изменения изучаются по результатам повторных астрономических наблюдений, геодезических измерений и гравиметрических определений. Предполагаемое горизонтальное движение материков изучают повторными астрономическими определениями положения отдельных точек земной поверхности. Повторные геодезические определения взаимного положения и высот точек земной поверхности через известные промежутки времени позволяют установить скорость и направление горизонтальных и вертикальных движений земной коры.

Схема триангуляции

  Разделы геодезии и виды геодезических работ. Область геодезических знаний делится на высшую геодезию и геодезию, которые сами подразделяются на более или менее самостоятельные разделы. Основной задачей высшей Геодезия является определение фигуры, размеров и гравитационного поля Земли, а также изучение теорий и методов её решения. В задачи высшей Геодезия входит также изучение теорий и методов основных геодезических работ, служащих для построения опорной геодезической сети и доставляющих данные для решения научных и практических задач Геодезия Геодезическая сеть представляет систему надлежаще выбранных и закрепленных на земной поверхности точек, называемых опорными геодезическими пунктами, взаимные положения и высоты которых определены в принятой системе координат и счёта высот. Положения опорных геодезических пунктов определяют преимущественно методом триангуляции, в основе которой лежит тригонометрический принцип измерения расстояний. Метод триангуляции состоит в построении на местности рядов и сетей треугольников, последовательно связанных между собой общими сторонами. Измерив в каком-нибудь из треугольников (рис. 2) одну сторону, называемую базисом или базисной стороной, и в каждом из них не менее 2 углов, длины сторон всех треугольников определяют путём тригонометрических вычислений. Обычно в каждом треугольнике измеряют все 3 угла, а в любой триангуляции, покрывающей значительную территорию, измеряют большое количество базисов, которые размещаются на определённом расстоянии друг от друга. Для построения геодезической сети применяется и метод полигонометрии, который состоит в измерении на местности длин последовательно связанных между собой линий, образующих полигонометрический ход, и горизонтальных углов между ними. Зная положение одного пункта и направление одной связанной с ним линии полигонометрического хода, путём вычислений последовательно определяют положение всех пунктов хода в принятой системе координат. Иногда положение опорных геодезических пунктов определяют методом трилатерации, измеряя все три стороны всех треугольников, образующих геодезическую сеть.

Геодезические пункты располагаются на возвышенных точках местности, которые выбирают рекогносцировкой. Каждый пункт закрепляется на местности закладкой на некоторую глубину бетонного блока с вделанной в него маркой, обозначающей вершину треугольника (см. Центр геодезический) (рис. 3), и постройкой деревянной или металлической вышки, служащей штативом для угломерного инструмента и визирной целью при измерении углов (см. Сигнал геодезический) (рис. 4). Иногда геодезические пункты совмещаются с наиболее выделяющимися местными предметами, такими, как водонапорные башни, шпили высоких зданий и т. и.

В зависимости от последовательности построения и точности измерений геодезической сети подразделяются на классы. Так, государственная геодезическая сеть СССР делится на I, II, III и IV классы. Государственная триангуляция I класса в СССР строится из рядов приблизительно равносторонних треугольников со сторонами 20—25 км, расположенных примерно по направлению земных меридианов и параллелей через 200—250 км. Пространства, ограниченные рядами триангуляции I класса, покрываются сплошными сетями треугольников II класса со сторонами около 10—20 км. Дальнейшее сгущение сети геодезических пунктов производится построением треугольников III и IV классов.

В местах пересечения рядов триангуляции I класса и в сетях триангуляции II класса измеряют базисы длиной не менее 5—6 км или базисные стороны. Базисы измеряют мерными проволоками (см. Базисный прибор) путём последовательного откладывания их по линии базиса, причём ошибки измерений не превышают 1:1000000 доли длины базиса. Базисные стороны измеряют непосредственно электрооптическими дальномерами с ошибкой не более 1:400000. Для измерения линий в полигонометрических ходах и сторон треугольников в трилатерации применяют также радиодальномеры.

  Углы треугольников и углы поворота полигонометрических ходов измеряют при помощи угломерных геодезических инструментов, представляющих собой сложные оптико-механические устройства. При этом под углом между направлениями на 2 наблюдаемых предмета в данной точке понимается угол между плоскостями, проходящими через эти предметы и отвесную линию в данной точке. Погрешности измерений углов треугольников в триангуляции I и II классов обычно не превышают 0,7».

Для построения сети опорных геодезических пунктов и определения их положения используют также результаты наблюдений за движением искусственных спутников Земли. Наблюдения спутника состоят либо в фотографировании его на фоне звёзд, положения которых известны, либо в измерениях расстояний до него с точек стояния при помощи радиотехнических средств или же в выполнении тех и других операций одновременно. Если законы движения спутника хорошо изучены, то он в этом случае служит подвижным геодезическим пунктом, координаты которого на каждый данный момент времени известны. Если же законы движения спутника не изучены, то он служит лишь промежуточным геодезическим пунктом, так что для определения неизвестной точки земной поверхности наблюдения спутника необходимо выполнять строго одновременно как в этой точке, так и в нескольких известных геодезических пунктах. Рассмотрение теорий и методов использования спутников для решения научных и практических задач Геодезия составляет содержание спутниковой геодезии.

  В конечных точках базисов и базисных сторон триангуляции I и II классов определяют широту и долготу этих точек, а также азимут направления на избранный земной предмет путём астрономических наблюдений (см. Лапласов пункт). Астрономические широты и долготы определяют также на промежуточных пунктах триангуляции I класса, выбираемых не реже чем 70—100 км. Астрономические определения на пунктах опорной геодезической сети превращают её в астрономо-геодезическую сеть, которая доставляет основные данные для исследований фигуры и размеров Земли и служит для распространения единой системы координат на всю территорию страны. Рассмотрение теории и методов определения географического положения места из астрономических наблюдений относится к геодезической астрономии.

  Плановое положение геодезических пунктов определяют геодезическими координатами, а именно I — широтами и долготами их проекций на поверхность некоторого земного эллипсоида — референц-эллипсоида. В каждом геодезическом пункте вместе с его координатами определяют также направления на смежные пункты относительно меридиана. Эти направления называют геодезическими азимутами и служат для ориентировки на местности.

Геодезические координаты одного из пунктов, являющегося исходным пунктом опорной геодезической сети, и геодезический азимут направления на один из смежных с ним пунктов устанавливают определением его астрономических координат и астрономического азимута того же направления исправлением их за влияние отклонения отвеса. Полученные данные, а также высота геоида над поверхностью референц-эллипсоида в исходном пункте характеризуют положение принятого эллипсоида в теле Земли и называются исходными геодезическими датами. Геодезические координаты и азимуты остальных пунктов получают путём вычисления по результатам геодезических измерений, приведённых к поверхности референц-эллипсоида.

Для вычисления координат пунктов государственной геодезической сети СССР принят референц-эллипсоид Красовского (см. Красовского эллипсоид), который характеризуется следующими данными:
большая полуось а = 6 37 8 245 м,
полярное сжатие a = 1:298,3,
а исходным пунктом служит Пулковская астрономическая обсерватория (центр её Круглого зала), причём для неё приняты следующие геодезические координаты:
широта В = 59° 4618,55»,
долгота L=30°19"42,09»,

полученные путём исправления её астрономической широты и долготы за влияние отклонения отвесной линии от нормали к поверхности эллипсоида Красовского. Высота геоида в Пулково над поверхностью этого эллипсоида принята равной нулю.

Один из разделов высшей Геодезия рассматривает геометрию земного эллипсоида и называется сфероидической Геодезия В её задачи входит разработка методов приведения геодезических измерений к поверхности референц-эллипсоида, методов решения треугольников и вычисления координат опорных пунктов на этой поверхности. Сфероидическая Геодезия даёт и математические основы методов определения фигуры и размеров Земли из градусных измерений.

Приведение геодезических измерений к поверхности референц-эллипсоида состоит в проектировании соответствующих пунктов на эту поверхность нормалями к ней. Это достигается тем, что в результаты геодезических измерений, например в длины линий и величины углов, вводятся поправки за высоту земной поверхности над поверхностью референц-эллипсоида и отклонения отвесной линии в определяемых пунктах.

Проекции определяемых пунктов на поверхности референц-эллипсоида соединяют геодезическими линиями, а их координаты получают последовательным вычислением и суммированием разностей координат каждых 2 смежных пунктов по длине и направлению соединяющей их геодезической линии (см. Геодезическая задача). Т. к. геодезические координаты выражаются в угловой мере и для практических целей неудобны, то они обычно заменяются прямоугольными координатами на плоскости путём отображения на ней поверхности референц-эллипсоида по тому или иному математическому закону точечного соответствия (см. Геодезические проекции). Сфероидическая Геодезия рассматривает теории отображения на плоскость только ограниченных частей поверхности земного эллипсоида. Отображение же всей поверхности земного эллипсоида на плоскость для построения географических карт рассматривается в математической картографии (см. Картографические проекции).

Высоты опорных геодезических пунктов определяют методами геометрического нивелирования, которое состоит в измерении и суммировании разностей высот каждых двух последовательных точек, расположенных на расстоянии (в зависимости от класса) 100—300 м одна от другой по некоторой линии, образующей нивелирный ход. Разности высот определяют нивелиром как разность отсчётов по имеющим точные деления рейкам, когда они установлены по отвесу, а визирная линия трубы нивелира строго горизонтальна. Линии геометрического нивелирования в зависимости от последовательности и точности выполнения работы подразделяются на классы.

В СССР нивелирование 1 класса производится по особо намеченным линиям, образующим замкнутые полигоны с периметром около 1600 км, и выполняется с наивысшей точностью, достижимой при применении современных инструментов и методов работы. Так, по линиям I класса случайная ошибка нивелирования не превышает 0,5 мм и систематическая ошибка составляет всего лишь 0,03 мм на 1 км нивелирного хода. Нивелирная сеть II класса строится из линий, прокладываемых вдоль железных, шоссейных, грунтовых дорог и больших рек и образующих замкнутые полигоны с периметром около 600 км. По линиям нивелирования II класса разности высот определяются со средней случайной ошибкой не более 1 мм и систематической — не более 0,2 мм на 1 км нивелирной линии. Нивелирные сети I и II классов сгущаются линиями нивелирования III и IV классов.

Линии нивелирования всех классов закрепляются на местности реперами или марками, которые закладываются через каждые 3—5 км в грунт, стены каменных зданий (рис. 5) и т. д. На линиях нивелирования I, II и III классов через 50—80 км и в местах их пересечения закладывают т. н. фундаментальные реперы, рассчитанные на долговременную сохранность. Высоты реперов и марок нивелирования вычисляют в той или иной системе высот над уровнем моря в каком-нибудь исходном пункте. В нивелирных работах СССР принята система нормальных высот, а исходным пунктом служит Кронштадтский футшток, нуль которого совпадает с многолетним средним уровнем Балтийского моря.

Для определения координат и высот пунктов опорной геодезической сети необходимы данные о распределении силы тяжести на земной поверхности. Вопросы измерения силы тяжести рассматриваются в гравиметрии, которая представляет собой самостоятельный раздел геодезических знаний. Методы использования гравиметрических данных для решения научных и практических задач Геодезия составляют содержание геодезической гравиметрии, созданной трудами советского учёного М. С. Молоденского.

В области геодезии рассматриваются методы, техника и организация работ, связанных с измерениями на земной поверхности для отображения её на планах и картах. Совокупность этих работ представляет топографическую съёмку местности и поэтому соответствующий раздел Геодезия часто называют топографией. В прошлом топографические съёмки производились наземным способом, который теперь применяется для съёмки лишь небольших участков местности. Топографические съёмки значительных площадей земной поверхности производятся путём сплошного фотографирования местности с летательных аппаратов (см. Аэрофотосъёмка) и последующей фотограмметрической обработки аэроснимков (см. Фотограмметрия). Результатом топографических съёмок являются топографические карты, которые служат исходным материалом для составления различных карт в более мелких масштабах. Методы составления и издания всевозможных карт рассматриваются в картографии.

  Изучение методов, техники и организации геодезических работ, связанных с проведением различных инженерных мероприятий (строительство гидротехнических сооружений, путей сообщения, крупных высотных зданий, промышленных предприятий и т. д.), составляет содержание инженерной геодезии. Рассмотрение аналогичных вопросов, относящихся к строительству шахт, тоннелей и метро, также входит в задачи инженерной Геодезия и вместе с тем является составной частью маркшейдерии.

  Т. к. геодезические измерения сопровождаются неизбежными ошибками различного характера, то в Геодезия принято каждую величину измерять многократно, а также измерять большее количество величин, чем необходимо для решения данной задачи. Измерение каждой избыточной величины создаёт одно условие, которое связывает её с другими величинами и которое не выполняется из-за их ошибок. Методы оценки точности геодезических измерений изучаются в теории ошибок (см. Наименьших квадратов метод), а приведение геодезических измерений в соответствие с теми математическими условиями, которым они должны удовлетворять, составляет содержание уравнительных вычислений.

  Краткие исторические сведения. Геодезия возникла в глубокой древности, когда появилась необходимость землеизмерения и составления планов и карт для хозяйственных целей. В 7 в. до н. э. в Вавилоне и Ассирии на глиняных дощечках составлялись географические карты, на которых давались сведения также и экономического характера. В 6—4 вв. до н. э. были высказаны предположения о шарообразности Земли и найдены некоторые доказательства этого. В 3 в. до н. э. в Египте греческий учёный Эратосфен произвёл первое определение радиуса земного шара на основании правильных геометрических принципов, получивших название градусных измерений. В это время в трудах Аристотеля впервые появилось название «Геодезия» как отрасли человеческих знаний, связанной с астрономией, картографией и географией. Во 2 в. до н. э. астрономы и математики установили понятия о географической широте и долготе места, разработали первые картографические проекции, ввели сетку меридианов и параллелей на картах, предложили первые методы определения взаимного положения точек земной поверхности из астрономических наблюдений. В начале 9 в. по поручению багдадского халифа Мамуна было произведено одно из первых градусных измерений вблизи Мосула и достаточно точно определён радиус земного шара.

Начало геодезических работ в России относится к 10 в. В сборнике законов «Русская правда» (11—12 вв.) содержатся постановления об определении земельных границ путём измерений. Одна из первых карт Московского государства, т. н. Большой чертёж, время составления которой относится к 16 в., основывалась на маршрутных съёмках и на опросных данных.

Развитие современной Геодезия и геодезических работ началось в 17 в. В начале 17 в. была изобретена зрительная труба. Большим шагом в развитии Геодезия явилось изобретение нидерландским учёным В. Снеллиусом в 1615—1617 метода триангуляции, который до сих пор служит одним из основных методов определения опорных пунктов для топографических съёмок. Появление угломерного инструмента, называемого теодолитом, и сочетание его со зрительной трубой, снабженной сеткой нитей, повысило точность угловых измерений в триангуляции. В середине 17 в. был изобретён барометр, явившийся первым инструментом для определения высоты точек земной поверхности. Были разработаны также графические методы топографической съёмки, упростившие составление топографических карт.

Открытие английским учёным И. Ньютоном закона всемирного тяготения во 2-й пол. 17 в. привело к возникновению идеи о сфероидичности Земли, т. е. сплюснутости её в направлении полюсов. Исходя из закона тяготения и гипотез о внутреннем строении Земли, И. Ньютон и нидерландский учёный X. Гюйгенс определили сжатие земного сфероида чисто теоретическим путём и получили сильно противоречивые результаты, вызвавшие сомнения в сплюснутости фигуры Земли и даже в обоснованности закона всемирного тяготения. В связи с этим в 1-й половине 18 в. Парижской АН были направлены в Перу и Лапландию геодезические экспедиции, которые произвели там градусные измерения, подтвердившие правильность идеи о сфероидичности Земли и доказавшие обоснованность закона всемирного тяготения. В середине 18 в. французский учёный А. Клеро разработал основы теории фигуры Земли и обосновал закон изменения силы тяжести на земном сфероиде в зависимости от географической широты. Эпоха открытия закона тяготения и упомянутых геодезических экспедиций явилась эпохой становления Геодезия как самостоятельной науки о фигуре Земли и методах её изучения. В конце 18 в. во Франции П. Мешен и Ж. Деламбр измерили дугу меридиана от Дюнкерка до Барселоны для установления длины метра как 1:10000000 доли четверти меридиана и получили один из первых достоверных выводов о размерах земного эллипсоида.

Развитие геодезических работ в России усилилось при Петре I, который в 1701 основал в Москве первую в России астрономическую обсерваторию и Школу математических и навигацких наук, готовившую математиков, астрономов, геодезистов и географов. Первые топографические съёмки в России были начаты на рубеже 17 и 18 вв. В 1720 Петр I топографические и картографические работы в России подчинил Сенату, подчеркнув тем самым их большое государственное значение. В 1739 в Петербургской АН был организован Географический департамент, который руководил всеми геодезическими и картографическими работами в России. По изданному в 1765 манифесту о генеральном межевании проводились геодезические работы по составлению планов землевладений, продолжавшиеся почти до середины 19 в. и доставившие обширный материал для картографирования страны. В 1779 в Москве возникла землемерная школа, которая в 1819 была преобразована в Константиновское землемерное училище, а в 1835 — в Константиновский межевой институт, позднее — крупное высшее учебное заведение по подготовке геодезистов и картографов. В связи с возросшими требованиями военного дела к топографическим картам в 1797 при Генеральном штабе было организовано Депо карт, которое в 1812 было преобразовано в Военно-топографическое депо, а в 1822 создан Корпус военных топографов. Все основные астрономо-геодезические и топографические работы в дореволюционной России выполнялись этим учреждением, труды которого являются замечательным памятником развития отечественной геодезической и картографической науки. В 1816 под руководством русского военного геодезиста К. И. Теннера и астронома В. Я. Струве в западных пограничных губерниях России были начаты большие астрономо-геодезические работы, которые в 1855 завершились градусным измерением огромной (более 25° по широте) дуги меридиана, простирающейся по меридиану 30° от устья Дуная до берегов Северного Ледовитого океана (рис. 6).

Немецкие учёные К. Ф. Гаусс в 1821—24 в Ганновере и Ф. В. Бессель в 1831—34 в Восточной Пруссии выполнили небольшие градусные измерения. Они усовершенствовали также методы и инструменты геодезических работ и разработали новые способы решения геодезических задач на поверхности земного эллипсоида. В 1828 Гаусс предложил принять за математическую поверхность Земли средний уровень моря. Русский военный геодезист Ф. Ф. Шуберт в 1859 впервые высказал мысль о возможной трёхосности Земли и определил размеры трёхосного земного эллипсоида. Немецкий физик И. Листинг в 1873 ввёл понятие о геоиде для обозначения фигуры Земли. В 1888 русский учёный Ф. А. Слудский создал оригинальную теорию фигуры Земли и обосновал некоторые методы её изучения.

В течение 19 в. был получен ряд определений размеров земного эллипсоида. Для успешного решения основной проблемы Геодезия в 1864 была создана Европейская, а затем и Международная комиссия по измерению Земли, которая явилась родоначальницей Международного геодезического и геофизического союза. Во 2-й половине 19 в. геодезические методы стали применяться для изучения внутреннего строения Земли и движений земной коры.

После Октябрьской революции наступила новая эпоха развития Геодезия и геодезических работ в нашей стране. По Декрету СНК РСФСР от 15 марта 1919, подписанному В. И. Лениным, было создано Высшее геодезическое управление, преобразованное впоследствии в Главное управление геодезии и картографии при Совете Министров СССР и являющееся центром государственной геодезической службы страны. Затем были образованы геодезические институты СССР и средние технические учебные заведения, выпускающие инженеров и техников по всем видам геодезических и картографических работ. В конце 1928 в Москве организован Центральный научно-исследовательский институт геодезии, аэросъёмки и картографии, превратившийся в крупнейший центр развития научной мысли в области геодезических знаний.

В 1928 сов. геодезист Ф. Н. Красовский разработал стройную и научно обоснованную схему и программу построения опорной геодезической сети, предусматривающую создание астрономо-геодезической сети на всей территории СССР. В ходе построения этой сети усовершенствовались теории, методы и инструменты астрономических определений и геодезических измерений. В СССР усовершенствован базисный прибор с подвесными мерными проволоками из инвара, освоено изготовление инварных мерных проволок с любым заданным коэффициентом расширения, разработаны оригинальные типы электрооптических дальномеров, радиодальномеров и радиогеодезических систем, позволяющих измерять расстояния с высокой точностью. Возникла промышленность, выпускающая астрономо-геодезические инструменты, аэросъёмочную аппаратуру и фотограмметрические приборы.

В 1932 по постановлению Совета труда и обороны СССР началась общая гравиметрическая съёмка страны, получившая впоследствии большое значение для решения научных и практических задач Геодезия и геофизики. Из исследований А. А. Михайлова, М. С. Молоденского и др. возникла геодезическая гравиметрия, являющаяся теперь важным разделом геодезических знаний. В связи с трудностями определения фигуры геоида М. С. Молоденский обосновал теорию изучения фигуры физической поверхности и внешнего гравитационного поля Земли. И. Д. Жонголович разработал методы определения фигуры, размеров и гравитационного поля Земли по наблюдениям искусственных спутников.

По градусным измерениям СССР и других стран Ф. Н. Красовский и А. А. Изотов в 1940 определили новые размеры земного эллипсоида, которые применяются теперь в СССР и других социалистических странах. Позднее А. А. Изотов и М. С. Молоденский определили ориентировку эллипсоида Красовского в теле Земли. В 1942—45 под руководством Д. А. Ларина было произведено общее уравнивание образовавшейся к тому времени обширной астрономо-геодезической сети СССР. Сов. геодезисты разработали методы уравнивания больших астрономо-геодезических сетей и сплошных сетей триангуляции (Ф. Н. Красовский, Н. А. Урмаев, И. Ю. Пранис-Праневич и др.).

Широкое развитие в СССР получили топографические съёмки и картографические работы, связанные с нуждами народного хозяйства и обороны страны. С 1925 в топографических съёмках стали применяться аэрофотосъёмка и фотограмметрические методы, разработанные советскими учёными (Ф. В. Дробышев, М. Д. Коншин, Геодезия В. Романовский и др.). В 1945 завершилась работа по созданию многолистной государственной топографической карты СССР в масштабе 1:1000000. Позднее была создана топографическая карта в масштабе 1:100000 на всю территорию страны, значительная часть которой покрыта съёмками и в более крупных масштабах.

Геодезические работы производились в связи с землеустройством, строительством городов, гражданских сооружений, промышленных предприятий, путей сообщения и т. д. Методы Геодезия применялись также при строительстве атомных электростанций, крупных ускорителей заряженных частиц и т. д.
Развитие Геодезия в СССР ознаменовалось постановкой и решением таких крупнейших научных проблем и практических задач, которые никогда не ставились в других странах.

Лит.: Руководства и монографии: Красовский Ф. Н. и Данилов В. В., Руководство по высшей геодезии, 2 изд., ч. 1, в. 1—2, М., 1938—39; Красовский Ф. Н., Руководство по высшей геодезии, ч. 2, М., 1942; Закатов П. С., Курс высшей геодезии, 3 изд., М., 1964; Чеботарев А. С., Геодезия, 2 изд., ч. 1, М., 1955; Чеботарев А. С., Селиханович В. Геодезия и Соколов М. Н., Геодезия, ч. 2, М., 1962; Гержула Б. И., Основы инженерной геодезии, М., 1960; Топография, под ред. Д. А. Слободчикова, ч. 1—2, М., 1954; Михайлов А. А., Курс гравиметрии и теории фигуры Земли, 2 изд., М., 1939; Бровар В. В., Магницкий В. А. и Шимбирев Б. П., Теория фигуры Земли, М., 1961; Шокин П. Ф., Гравиметрия, М., 1960; Молоденский М. С., Юркина М. И. и Еремеев В. Ф., Методы изучения внешнего гравитационного поля и фигуры Земли, «Тр. Центрального научно-исследовательского института геодезии, аэросъемки и картографии», 1960, в. 131; Изотов А. А., Форма и размеры Земли по современным данным, там же, 1950, в. 73; Елисеев С. В., Геодезические инструменты и приборы, 2 изд., М., 1959; Чеботарев А. С., Способ наименьших квадратов с основами теории вероятностей, М., 1958; Пранис-Праневич И. Ю., Руководство по уравнительным вычислениям триангуляции, 2 изд., М., 1956; Вейс Геодезия, Геодезическое использование искусственных спутников Земли, пер. с англ., М., 1967; Меллер И., Введение в спутниковую геодезию, пер. с англ., М., 1967; Беррот А. и Хофман В., Космическая геодезия, пер. с нем., М., 1963; Helmert F. R., Die mathematischen und physikalischen Theorien der höheren Geodäsie, 2 Aufl., Bd 1—2, Lpz., 1962; Jordan W., Eggert О., Kneissl М., Handbuch der Vermessungskunde, 10 Aufl., Bd 1—4, Stuttg., 1955—61; Ryšavy J., Vyšši geodesie, Praha, 1947.

  История. Котельников С. К., Молодой геодет, или первые основания геодезии, содержащие все геодетское знание, предложенное вкратце, изъясненное правилами и примерами, СПБ, 1766; Болотов А. П., Курс высшей и низшей геодезии, ч. 1—2, СПБ, 1845—49; Струве В. Я., Дуга меридиана, т. 1—2, СПБ, 1861; Евтеев О. А., Первые русские геодезисты на Тихом океане, М., 1950; 50 лет советской геодезии и картографии, под ред. А. Н. Баранова и М. К. Кудрявцева, М., 1967; Бируни, Геодезия, Избр. произв., т. 3, Таш., 1966.

  Справочники. Геодезия. Справочное руководство, под ред. М. Д. Бонч-Бруевича, т. 1—9, М. — Л., 1939—1949; Справочник геодезиста, под ред. В. Д. Большакова и Геодезия П. Левчука, М., 1966: Библиографический указатель геодезической литературы с начала книгопечатания до 1917 г., сост. Е. Ф. Беликов, Л. П. Соловьев, М., 1971.
А. А. Изотов.

Рис. 4. Геодезический сигнал.


Рис. 5. Нивелирный репер, заложенный в стене здания.


Рис. 2. Схема триангуляции.


Рис. 3. Разрез подземного центра геодезического пункта.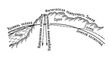


Рис. 1. Разрез земной поверхности вертикальной плоскостью.


Рис. 6. Монумент на южном конце дуги меридиана Струве (Старо-Некрасовка, близ Измаила) с надписью: «Южный предел Дуги меридиaна 25° 20" от реки Дунай до Океана Ледовитого чрез Pocсию, Швецию и Норвегию... Постоянно трудясь с 1816 по 1852 измерили геометры трех народов. Широта 45° 20" 28"».