


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Гильбертово пространство
Определение "Гильбертово пространство" в Большой Советской Энциклопедии
Гильбертово пространство, математическое понятие, обобщающее понятие евклидова пространства на бесконечномерный случай. Возникло на рубеже 19 и 20 вв. в виде естественного логического вывода из работ нем. математика Гильберта в результате обобщения фактов и методов, относящихся к разложениям функций в ортогональные ряды и к исследованию интегральных уравнений. Постепенно развиваясь, понятие «Гильбертово пространство» находило все более широкие приложения в различных разделах математики и теоретической физики; оно принадлежит к числу важнейших понятии математики.
Первоначально Гильбертово пространство понималось как пространство последовательностей со сходящимся рядом квадратов (т. н. пространство l2). Элементами (векторами) такого пространства являются бесконечные числовые последовательности
x = (x1, x2,..., xn,...)
такие, что ряд x21 + x22 +... + х2n + ... сходится. Сумму двух векторов х + y и вектор lx, где l - действительное число, определяют естественным образом:
x + y = (x1 + y1,..., xn + yn,...),
lx = (lx1, lx2, ..., lxn,...)/
Для любых векторов х, y Î l2 формула
(x, y) = x1y1 + x2y2 + ... +xnyn + ...
определяет их скалярное произведение, а под длиной (нормой) вектора х понимается неотрицательное число

Скалярное произведение всегда конечно и удовлетворяет неравенству |(х, у)| £ ||x|| ||y||. Последовательность векторов хn называется сходящейся к вектору х, если ||хn-х|| ® 0 при n ® ¥. Многие определения и факты теории конечномерных евклидовых пространств переносятся и на Гильбертово пространство Например, формула
где 0 £ j £ p определяет угол j между векторами х и у. Два вектора х и у называются ортогональными, если (х, у) = 0. Пространство l2 полно: всякая фундаментальная последовательность Коши элементов этого пространства (т. е. последовательность хn, удовлетворяющая условию ||хп-хm||® 0 при n, m ® ¥) имеет предел. В отличие от евклидовых пространств, Гильбертово пространство l2 бесконечномерно, т. е. в нём существуют бесконечные системы линейно независимых векторов; например, такую систему образуют единичные векторы
e1 = (1, 0, 0,...), e2 = (0, 1, 0,...),...
При этом для любого вектора x из l2 имеет место разложение
x = x1e1 + x2e2 +... (1)
по системе {en}.
Другим важным примером Гильбертово пространство служит пространство l2 всех измеримых функций, заданных на некотором отрезке [a, b], для которых конечен интеграл

понимаемый как интеграл в смысле Лебега. При этом функции, отличающиеся друг от друга лишь на множество меры нуль, считаются тождественными. Сложение функций и умножение их на число определяется обычным способом, а под скалярным произведением понимается интеграл
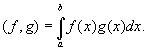
Норма в этом случае равна
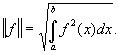
Роль единичных векторов предыдущего примера здесь могут играть любые функции ji(x) из L2, обладающие свойствами ортогональности
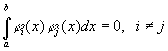
и нормированности

а также следующим свойством замкнутости: если f(x) принадлежит L2 и

то f(x) = 0 всюду, кроме множества меры нуль. На отрезке [0,2p] в качестве такой системы функций можно взять тригонометрическую систему

Разложению (1) соответствует разложение функции f(x) из L2 в ряд Фурье
сходящийся к f(x) по норме пространства L2. При этом для всякой функции f(x) выполняется равенство Парсеваля

Соответствие между функциями f(x) из L2 и последовательностями их коэффициентов Фурье a0, a1, b1, a2, b2,... является взаимно однозначным отображением L2 на l2, сохраняющим операции сложения, умножения на числа, а также сохраняющим длины и скалярные произведения. Т. о., эти пространства изоморфны и изометричны, значит имеют одинаковое строение.
В более широком смысле под Гильбертово пространство понимают произвольное линейное пространство, в котором задано скалярное произведение и которое является полным относительно нормы, порождаемой этим скалярным произведением. В зависимости от того, определено ли для элементов Гильбертово пространство Н умножение только на действительные числа или же элементы из Н можно умножать на произвольные комплексные числа, различают действительное и комплексное Гильбертово пространство В последнем случае под скалярным произведением понимают комплексную функцию (х, у), определённую для любой пары х, у элементов из Н и обладающую следующими свойствами:
1) (х, х) = 0 в том и только том случае, если х = 0,
2) (х, х) ³ 0 для любого x из Н,
3) (х + у, z) = (x, z) + (у, z),
4) (lx, у) = l(x, у) для любого комплексного числа l,
5) 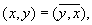
где черта означает комплексно сопряжённую величину. Норма элемента х определяется равенством

Комплексные Гильбертово пространство играют в математике и в её приложениях значительно большую роль, чем действительные Гильбертово пространство Одним из важнейших направлений теории Гильбертово пространство является изучение линейных операторов в Гильбертово пространство (см. Операторов теория). Именно с этим кругом вопросов связаны многочисленные применения Гильбертово пространство в теории дифференциальных и интегральных уравнений, теории вероятностей, квантовой механике и т. д.
Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; Данфорд Н., Шварц Дж., Линейные операторы, т. 1 - Общая теория, пер. с англ., М., 1962; Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961.
Ю. В. Прохоров.
| "БСЭ" >> "Г" >> "ГИ" >> "ГИЛ" |
Статья про "Гильбертово пространство" в Большой Советской Энциклопедии была прочитана 969 раз
| Коптим скумбрию в коробке |
| Креветки с газировкой |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная