


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Линейное пространство
Определение "Линейное пространство" в Большой Советской Энциклопедии
Линейное пространство, тоже, что векторное пространство. В функциональном анализе рассматриваются главным образом бесконечномерные пространства. Примером бесконечномерного Линейное пространство может служить пространство всех многочленов (с вещественными или комплексными коэффициентами) при обычном определении сложения и умножения на числа. Одним из первых примеров бесконечного Линейное пространство были гильбертово пространство и пространство С [а, b] непрерывных функций, заданных на отрезке [а, b]. Эти пространства являются нормированными, т. е. такими Линейное пространство, в которых введена норма элемента х — неотрицательное число 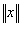 , обращающееся в нуль лишь при х = 0 и обладающее свойствами
, обращающееся в нуль лишь при х = 0 и обладающее свойствами 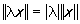 и
и 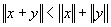 (неравенство треугольника). Число
(неравенство треугольника). Число 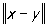 называют расстоянием между элементами х и у (см. также Метрическое пространство). В нормированном Линейное пространство вводятся понятия открытого шара, предельной точки множества, непрерывности функционала аналогично тому, как это делается в трёхмерном пространстве.
называют расстоянием между элементами х и у (см. также Метрическое пространство). В нормированном Линейное пространство вводятся понятия открытого шара, предельной точки множества, непрерывности функционала аналогично тому, как это делается в трёхмерном пространстве.
В конечномерном пространстве различные нормы топологически равносильны: последовательность точек, сходящихся при одной норме, сходится и при любой другой. В бесконечномерных пространствах нормы могут быть существенно различны. Например, при решении задачи П. Л. Чебышева о разыскании многочлена, наименее уклоняющегося от нуля (задачи о наилучшем приближении), надо найти такой многочлен (k — 1)-й степени Pk-i(t), чтобы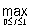
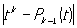
имел наименьшее значение. Вводя в пространство С[0,1] норму формулой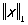 =
= 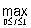
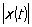
эту задачу можно сформулировать следующим образом: требуется найти многочлен Pk-i(t), расстояние которого от функции t* было бы наименьшим. При рассмотрении же многочленов, ортогональных с весом p(t) (см. Ортогональная система функций), естественно рассматривать норму, определённую формулой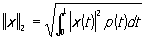 ,
,
и решать задачу о наилучшем приближении в смысле этой нормы. Нормы 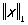 и
и 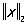 существенно различны, так как, например, последовательность функций
существенно различны, так как, например, последовательность функций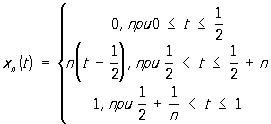
по первой норме расходится, а по второй норме при p(t) = 1 сходится к функции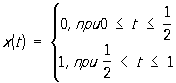 .
.
Следует отметить, что хотя все функции xn(t) были непрерывны, функция x(t) разрывна. Это связано с тем, что пространство непрерывных функций неполно относительно нормы 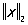 . При этом нормированное Линейное пространство называется полным, если для любой последовательности {xn} его элементов, удовлетворяющих условию
. При этом нормированное Линейное пространство называется полным, если для любой последовательности {xn} его элементов, удовлетворяющих условию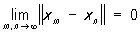 ,
,
существует в Линейное пространство такой элемент х, что данная последовательность сходится к нему, т. е.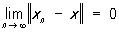 ,
,
Если Линейное пространство неполно, то к нему можно присоединить новые элементы (пополнить его) так, что оно станет полным. Например, пополняя пространство непрерывных функций, взятое с нормой 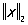 , получают гильбертово пространство L2p. Полные нормированные Линейное пространство называется банаховыми, или В-пространствами, — по имени изучившего их основные свойства С. Банаха.
, получают гильбертово пространство L2p. Полные нормированные Линейное пространство называется банаховыми, или В-пространствами, — по имени изучившего их основные свойства С. Банаха.
Обобщением понятия B-пространства является понятие топологического Линейное пространство Так, называют множество Е, если: 1) оно представляет собой Линейное пространство, 2) оно является топологическим пространством, 3) операции сложения и умножения на числа в Е непрерывны относительно заданной в Е топологии. К числу топологического Линейное пространство относятся все нормированные пространства. А. Н. Колмогоров установил (1934) необходимые и достаточные условия нормируемости топологического Линейное пространство
Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965.
| "БСЭ" >> "Л" >> "ЛИ" >> "ЛИН" >> "ЛИНЕ" |
Статья про "Линейное пространство" в Большой Советской Энциклопедии была прочитана 838 раз
| Пицца в сковороде |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная