


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Деление (математич.)
Определение "Деление (математич.)" в Большой Советской Энциклопедии
Деление, действие, обратное умножению; заключается в нахождении одного из двух сомножителей, если известны произведение их и др. сомножитель. Т. о., разделить а на b - это значит найти такое х, что bx = а или xb = а. Результат Деление (математич.) х называется частным, или отношением, a и b. Заданное произведение а называется делимым, а заданный множитель b - делителем. Для обозначения Деление (математич.) употребляют знаки двоеточия (а: b) или горизонтальной (иногда наклонной) черты (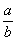 , a/b).
, a/b).
В пределах системы целых чисел Деление (математич.) не всегда возможно (6 делится на 2 и 3, но не делится на 5, см. Делимость), но в тех случаях, когда оно возможно, результат его всегда определён единственным образом (как говорят, однозначно). В системе всех рациональных чисел (т. е. чисел целых и дробных) Деление (математич.) не только однозначно, но и всегда осуществимо, за единственным исключением - Деление (математич.) на нуль. Если исходить из данного выше определения Деление (математич.), то легко видеть, что Деление (математич.) числа, отличного от нуля, на нуль невозможно. Результатом Деление (математич.) нуля на нуль, по определению, может быть любое число (т.к. всегда с·0 = 0). Обычно в алгебре предпочитают (чтобы не нарушать однозначности Деление (математич.)) считать, что Деление (математич.) на нуль невозможно во всех случаях.
От точного Деление (математич.), которое до сих пор рассматривалось, отличается Деление (математич.) с остатком. Это, по существу, совершенно особая операция, отличная от Деление (математич.) в определённом выше смысле. Если а и b - целые неотрицательные числа, то операция Деление (математич.) с остатком числа а на число b состоит в определении целых неотрицательных чисел х и у, удовлетворяющих требованиям:
1) а = xb + у,
2) у < b.
При этом а называется делимым, b - делителем, х - частным, у - остатком. Эта операция всегда осуществима и всегда однозначна. Если у = 0, то говорят, что а делится на b без остатка. Аналогично определяется операция Деление (математич.) с остатком для многочленов вида
P (x) = a0xn + a1xn-1 +...+ an.
Она состоит в нахождении по двум многочленам Р(х) и Q(x) двух многочленов S(x) и R(x), удовлетворяющих требованиям:
1) Р (х) = S (x) Q (x) + R (x);
2) степень R (x) меньше степени Q (x). Эта операция также всегда осуществима и однозначна. Если R (x) º 0, то Р (х) делится на Q (x) без остатка.
Лит.: Депман И. Я., История арифметики, 2 изд., М., 1965; Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968.
| "БСЭ" >> "Д" >> "ДЕ" >> "ДЕЛ" |
Статья про "Деление (математич.)" в Большой Советской Энциклопедии была прочитана 700 раз
| Бургер двойного помола |
| Яйца в кляре |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная