


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Умножение
Определение "Умножение" в Большой Советской Энциклопедии
Умножение, операция образования по двум данным объектам а и b, называемым сомножителями, третьего объекта с, называемого произведением. Умножение обозначается знаком Х (ввёл англ. математик Умножение Оутред в 1631) или • (ввёл нем. учёный Г. Лейбниц в 1698); в буквенном обозначении эти знаки опускаются и вместо а ´ b или а • b пишут ab. Умножение имеет различный конкретный смысл и соответственно различные конкретные определения в зависимости от конкретного вида сомножителей и произведения. Умножение целых положительных чисел есть, по определению, действие, относящее числам а и b третье число с, равное сумме b слагаемых, каждое из которых равно а, так что ab = а + а +... + а (b слагаемых). Число а называется множимым, b – множителем. Умножение дробных чисел  и
и 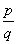 определяется равенством
определяется равенством 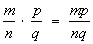 (см. Дробь). Умножение рациональных чисел даёт число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (–), если они разного знака. Умножение иррациональных чисел определяется при помощи Умножение их рациональных приближений. Умножение комплексных чисел, заданных в форме a = а + bi и b = с + di, определяется равенством ab = ac – bd + (ad + bc) i. При Умножение комплексных чисел, записанных в тригонометрической форме:
(см. Дробь). Умножение рациональных чисел даёт число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (–), если они разного знака. Умножение иррациональных чисел определяется при помощи Умножение их рациональных приближений. Умножение комплексных чисел, заданных в форме a = а + bi и b = с + di, определяется равенством ab = ac – bd + (ad + bc) i. При Умножение комплексных чисел, записанных в тригонометрической форме:
a = r1 (cosj1 + isin j1),
b = r2 (cosj2 + isin j2),
их модули перемножаются, а аргументы складываются:
ab = r1r2{cos (j1 + j2) + i sin ((j1 + j2)}.
Умножение чисел однозначно и обладает следующими свойствами:
1) ab = ba (коммутативность, переместительный закон);
2) a (bc) = (ab) c (ассоциативность, сочетательный закон);
3) a (b + c) = ab + ac (дистрибутивность, распределительный закон). При этом всегда а ×0 = 0; a×1 = а. Указанные свойства лежат в основе обычной техники Умножение многозначных чисел.
Дальнейшее обобщение понятия Умножение связано с возможностью рассматривать числа как операторы в совокупности векторов на плоскости. Например, комплексному числу r (cosj + i sin j) соответствует оператор растяжения всех векторов в r раз и поворота их на угол j вокруг начала координат. При этом Умножение комплексных чисел отвечает Умножение соответствующих операторов, т. е. результатом Умножение будет оператор, получающийся последовательным применением двух данных операторов. Такое определение Умножение операторов переносится и на другие виды операторов, которые уже нельзя выразить при помощи чисел (например, линейные преобразования). Это приводит к операциям Умножение матриц, кватернионов, рассматриваемых как операторы поворота и растяжения в трёхмерном пространстве, ядер интегральных операторов и т.д. При таких обобщениях могут оказаться невыполненными некоторые из перечисленных выше свойств Умножение, чаще всего – свойство коммутативности (некоммутативная алгебра). Изучение общих свойств операции Умножение входит в задачи общей алгебры, в частности теории групп и колец.
| "БСЭ" >> "У" >> "УМ" |
Статья про "Умножение" в Большой Советской Энциклопедии была прочитана 1009 раз
| Коптим скумбрию в коробке |
| Кетчуп из бананов |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная