


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Исчерпывания метод
Определение "Исчерпывания метод" в Большой Советской Энциклопедии
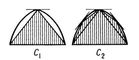 |
| Исчерпывания метод. Рис. |
Типичная схема доказательства при помощи Исчерпывания метод может быть изложена в современных обозначениях так: для определения величины А строится некоторая последовательность величин C1, C2, ..., Cn, ... так, что
Cn < A; (1)
предполагают также известным такое В, что
Cn < В (2)
и при любом целом К для достаточно больших n удовлетворяются неравенства
К (A — Cn) < D, К (В — Cn) < D, (3)
где D — постоянно. С современной точки зрения, для перехода от неравенств (3) к равенству
А = В (4)
достаточно заметить, что из условий (1), (2) и (3) следует
Математики древности, не располагавшие теорией пределов, обращались к доказательству от противного и доказывали невозможность каждого из неравенств А < В, В < А. Чтобы опровергнуть первое из них, при помощи аксиомы Евдокса — Архимеда (см. Архимеда аксиома) устанавливали, что для R = B — А существует такое К, что KR > D и в силу условия (1) получали
К (В — Cn) > К (В — A) > D,
что противоречит второму из неравенств (3). Аналогично опровергалось другое предположение. После этого оставалось принять только равенство (4).
Введение Исчерпывания метод вместе с лежащей в его основе аксиомой приписывается Евдоксу Книдскому. Этим методом широко пользовался Евклид, а с особенным искусством и разнообразием — Архимед. Например, для определения площади сегмента А параболы Архимед строит площади C1, C2, ..., «исчерпывающие» при их постепенном нарастании площадь A сегмента, по схеме, ясной из чертежа. При этом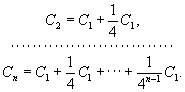
Вместо того чтобы прибегнуть к предельному переходу,
Архимед геометрически доказывает, что при любом n
Вводя площадь
Архимед получает, что
и, следуя изложенному выше порядку, заканчивает доказательство того, что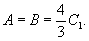
| "БСЭ" >> "И" >> "ИС" >> "ИСЧ" |
Статья про "Исчерпывания метод" в Большой Советской Энциклопедии была прочитана 899 раз
| Бургер двойного помола |
| Яйца в кляре |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная