БОЛЬШАЯ СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, БСЭ БОЛЬШАЯ СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, БСЭ
Навигация:
Библиотека DJVU
БСЭ
 Статистика:

Квадратное уравнение

Значение слова "Квадратное уравнение" в Большой Советской Энциклопедии

Квадратное уравнение, уравнение вида ax2 + bx + с = 0, где а, b, с - какие-либо числа, называются коэффициентами уравнения. Квадратное уравнение имеет два корня, которые находятся по формулам: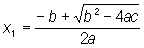





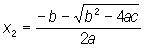
  Выражение D = b2 - 4ac называется дискриминантом Квадратное уравнение Если D > 0, то корни Квадратное уравнение действительные различные, если D < 0, то корни сопряжённые комплексные, если D = 0, то корни действительные равные. Имеют место формулы Виета: x1 +х2 = -b/a, x1x2 = с/а, связывающие корни и коэффициенты Квадратное уравнение Левую часть Квадратное уравнение можно представить в виде а (х - х1)(х - x2). Функцию у = ax2 + bx + с называют квадратным трёхчленом, её графиком служит парабола с вершиной в точке М (-b/2a; с  - b2/4a) и осью симметрии, параллельной оси Оу; направление ветвей параболы совпадает со знаком a. Решение Квадратное уравнение было известно в геометрической форме ещё математикам древности.

В Большой Советской Энциклопедии рядом со словом "Квадратное уравнение"

Квадратное письмо | Буква "К" | В начало | Буквосочетание "КВ" | Квадратура (матем.)


Статья про слово "Квадратное уравнение" в Большой Советской Энциклопедии была прочитана 0 раз

Интересное

  • Florists in america
  • business support in USA
    •