


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Квадратура круга
Определение "Квадратура круга" в Большой Советской Энциклопедии
Квадратура круга, задача о разыскании квадрата, равновеликого данному кругу. Под Квадратура круга понимают как задачу точного построения квадрата, равновеликого кругу, так и задачу вычисления площади круга с тем или иным приближением. Задачу о точной Квадратура круга пытались решить первоначально с помощью циркуля и линейки. Математика древности знала ряд случаев, когда с помощью этих инструментов удавалось преобразовать криволинейную фигуру в равновеликую ей прямолинейную (см., например, Гиппократовы луночки). Попытки решения задачи о Квадратура круга, продолжавшиеся в течение тысячелетий, неизменно оканчивались неудачей. С 1775 Парижская АН, а затем и др. академии стали отказываться от рассмотрения работ, посвященных Квадратура круга Лишь в 19 в. было дано научное обоснование этого отказа: строго установлена неразрешимость Квадратура круга с помощью циркуля и линейки.
Если радиус круга равен г, то сторона равновеликого этому кругу квадрата равна 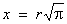 . Таким образом, задача сводится к следующей: осуществить построение, в результате которого данный отрезок (r) был бы умножен на данное число (
. Таким образом, задача сводится к следующей: осуществить построение, в результате которого данный отрезок (r) был бы умножен на данное число (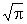 ). Однако графическое умножение отрезка на число осуществимо циркулем и линейкой, если упомянутое число — корень алгебраического уравнения с целыми коэффициентами, разрешимого в квадратных радикалах. Т. о., окончательная ясность в вопросе о Квадратура круга могла быть достигнута на пути изучения арифметической природы числа p. В конце 18 в. нем. математиком И. Ламбертом и французским математиком А. Лежандром была установлена иррациональность числа p. В 1882 нем. математик Ф. Линдеман доказал, что число p (а значит и
). Однако графическое умножение отрезка на число осуществимо циркулем и линейкой, если упомянутое число — корень алгебраического уравнения с целыми коэффициентами, разрешимого в квадратных радикалах. Т. о., окончательная ясность в вопросе о Квадратура круга могла быть достигнута на пути изучения арифметической природы числа p. В конце 18 в. нем. математиком И. Ламбертом и французским математиком А. Лежандром была установлена иррациональность числа p. В 1882 нем. математик Ф. Линдеман доказал, что число p (а значит и 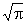 ) трансцендентно, т. е. не удовлетворяет никакому алгебраическому уравнению с целыми коэффициентами. Теорема Линдемана положила конец попыткам решения задачи о Квадратура круга с помощью циркуля и линейки. Задача о Квадратура круга становится разрешимой, если расширить средства построения. Уже греч. геометрам было известно, что Квадратура круга можно осуществить, используя трансцендентные кривые; первое решение задачи о Квадратура круга было выполнено Диностратом (4 в. до н. э.) при помощи специальной кривой — так называемые квадратрисы (см. Линия). О задаче нахождения приближённого значения числа p см. в ст. Пи.
) трансцендентно, т. е. не удовлетворяет никакому алгебраическому уравнению с целыми коэффициентами. Теорема Линдемана положила конец попыткам решения задачи о Квадратура круга с помощью циркуля и линейки. Задача о Квадратура круга становится разрешимой, если расширить средства построения. Уже греч. геометрам было известно, что Квадратура круга можно осуществить, используя трансцендентные кривые; первое решение задачи о Квадратура круга было выполнено Диностратом (4 в. до н. э.) при помощи специальной кривой — так называемые квадратрисы (см. Линия). О задаче нахождения приближённого значения числа p см. в ст. Пи.
Лит.: О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). С приложением истории вопроса, пер. с нем., 3 изд., М. — Л., 1936; Стройк Д. Я., Краткий очерк истории математики, пер. с нем.,2 изд., М., 1969.
| "БСЭ" >> "К" >> "КВ" >> "КВА" >> "КВАД" |
Статья про "Квадратура круга" в Большой Советской Энциклопедии была прочитана 820 раз
| Коптим скумбрию в коробке |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная