


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Кеплера уравнение
Определение "Кеплера уравнение" в Большой Советской Энциклопедии
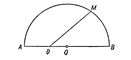 |
| Кеплера уравнение. Рис. |
у—с siny=x.
Для приложений важен случай | с | < 1, когда у определяется по заданным с и х единственным образом. Кеплера уравнение впервые рассматривалось И. Кеплером («Новая астрономия», 1609) в связи с задачей: на диаметре АВ полукруга АОВМ дана точка D; провести прямую DM так, чтобы она делила площадь полукруга в заданном отношении (см. рис.). Кеплера уравнение играет важную роль в астрономии при определении элементов эллиптических орбит планет. В небесной механике это уравнение обычно записывают в форме
Е—е sin Е=М,
где е — эксцентриситет эллипса, М — средняя аномалия, Е — эксцентрическая аномалия (см. Орбиты небесных тел). Решением Кеплера уравнение занимались также Ж. Лагранж (1771), П. Лаплас (1823), Ф. Бессель (1816—17), К. Гаусс (1809) и др.
Лит.: Субботин М. Ф. Курс небесной механики, 2 изд., т. 1, Л. — М., 1941.
| "БСЭ" >> "К" >> "КЕ" >> "КЕП" |
Статья про "Кеплера уравнение" в Большой Советской Энциклопедии была прочитана 734 раз
| Коптим скумбрию в коробке |
| Куриный суп |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная