Орбиты небесных тел

Определение "Орбиты небесных тел" в Большой Советской Энциклопедии

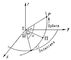Эллиптическая орбита планеты в пространстве

Орбиты небесных тел, траектории, по которым движутся небесные тела в космическом пространстве. Формы Орбиты небесных тел и скорости, с которыми по ним движутся небесные тела, определяются силой тяготения, а также силой светового давления, электромагнитными силами, сопротивлением среды, в которой происходит движение, приливными силами, реактивными силами (в случае движения ядра кометы) и многое др. В движении планет, комет и спутников планет, а также в движении Солнца и звёзд в Галактике решающее значение имеет сила всемирного тяготения. На активных участках орбит искусственных космических объектов наряду с силами тяготения определяющее значение имеет реактивная сила двигательной установки. Ориентация орбиты в пространстве, её размеры и форма, а также положение небесного тела на орбите определяются величинами (параметрами), называемыми элементами орбиты. Элементы орбит планет, комет и спутников определяются по результатам астрономических наблюдений в три этапа: 1) вычисляются элементы т. н. предварительной орбиты без учёта возмущений (см. Возмущения небесных тел), т. е. решается двух тел задача. Для этой цели в большинстве случаев достаточно иметь три наблюдения (т. е. координаты трёх точек на небесной сфере) небесного тела (например, малой планеты), охватывающие промежуток времени в несколько дней или недель. 2) Осуществляется улучшение предварительной орбиты (т. е. вычисляются более точные значения элементов орбиты) по результатам более длительного ряда наблюдений. 3) Вычисляется окончательная орбита, которая наилучшим образом согласуется со всеми имеющимися наблюдениями.

Для многих тел Солнечной системы, в том числе для больших планет, Луны и некоторых спутников планет, имеются уже длительные ряды наблюдений. Для вычисления по этим наблюдениям окончательной орбиты (или, как говорят, для разработки теории движения небесного тела) применяются аналитические и численные методы небесной механики.

  В результате первого этапа орбита определяется в виде конического сечения (эллипса, иногда также параболы или гиперболы), в фокусе которого находится другое (центральное) тело. Такие орбиты называются невозмущёнными или кеплеровыми, т.к. движение небесного тела по ним происходит по Кеплера законам. Шестью элементами, определяющими гелиоцентрическую невозмущённую Орбиты небесных тел Р (рис.), являются: 1) наклон орбиты к плоскости эклиптики i. Может иметь любое значение от 0 до 180°; наклон считается меньшим 90°, если для наблюдателя, находящегося в северном полюсе эклиптики, движение планеты имеет прямое направление (против часовой стрелки), и большим 90° при обратном движении. 2) Долгота узла W. Это — гелиоцентрическая долгота точки, в которой планета пересекает эклиптику, переходя из Южного полушария в Северное (восходящий узел орбиты). Долгота узла может принимать значения от 0 до 360°. 3) Большая полуось орбиты а. Иногда вместо а в качестве элемента орбиты принимается среднее суточное движение n (дуга орбиты, проходимая телом за сутки). 4) Эксцентриситет орбиты е. Если b – малая полуось орбиты, то е = 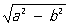/a. Вместо эксцентриситета иногда принимают угол эксцентриситета j, который определяется соотношением sin j = е. 5) Расстояние перигелия от узла (или аргумента перигелия) w. Это гелиоцентрический угол между восходящим узлом орбиты и направлением на перигелий орбиты, измеряемый в плоскости орбиты в направлении движения планеты; может иметь любые значения от 0 до 360°. Вместо элемента w применяется также долгота перигелия p = W + w. 6) Элемент времени, т. е. эпоха (дата), в которую планета находится в определённой точке орбиты. В качестве такого элемента может служить, например, момент t, в который планета проходит перигелий. Положение планеты на орбите определяется аргументом широты и, который представляет собой угловое расстояние планеты вдоль орбиты от восходящего узла, или истинной аномалией v — угловым расстоянием планеты от перигелия. Аргумент широты меняется от 0 до 360° в направлении движения планеты. Аналогичными элементами определяются орбиты комет, Луны, спутников планет, компонентов двойных звёзд, Солнца в Галактике и др. небесных тел. Однако вместо термина «перигелий» в этих случаях употребляется или более общий термин — «перицентр», или специализированные название «перигей» (для Луны, движущейся по геоцентрической орбите), «периастр» (для компонентов двойной звезды) и т.п.

Задача улучшения (уточнения) предварительной орбиты при помощи дополнительных наблюдений решается путём последовательных приближений. Чем больше интервал времени, охватываемый наблюдениями, тем надёжнее определяются элементы улучшенной орбиты. В реальном случае, когда действуют не только силы тяготения, но и др. (возмущающие) силы, движение небесного тела не соответствует законам Кеплера. Однако отклонение движения от невозмущённого невелико и поэтому его описывают формулами невозмущённого движения, но при этом предполагают, что элементы орбиты не сохраняют постоянные значения, а изменяются с течением времени. Т. о. реальная орбита рассматривается как огибающая семейства непрерывно изменяющихся кеплеровых орбит; при этом в каждый момент времени положение и скорость небесного тела на реальной орбите совпадают со значениями положения и скорости, которые небесное тело имело бы, двигаясь по кеплеровой орбите с элементами, вычисленными именно для этого момента. Орбита, определённая таким методом для заданного момента времени t, называется оскулирующей орбитой, а момент t — эпохой оскуляции. Оскулирующая орбита непрерывно изменяет своё положение в пространстве и форму.

Метод определения первоначальной параболической орбиты был разработан Г. Ольберсом (1797), а эллиптической — К. Гауссом (1809). Методам улучшения орбит и определения окончательных орбит были посвящены многочисленные работы в 19—20 вв. Элементы орбит планет, малых планет, комет регулярно публикуются в астрономических ежегодниках и др. изданиях.

Классические методы небесной механики с успехом применяются также и для вычисления орбит искусственных спутников Земли (ИСЗ). В этом случае учитываются вековые изменения большой полуоси орбиты, долготы узла и аргумента широты, вызываемые тормозящим воздействием атмосферы, несферичностью Земли, а в некоторых случаях и световым давлением Солнца. Радиотехнические, радиолокационные и лазерные дальномерные методы наблюдений ИСЗ позволяют непосредственно определять расстояния до спутника и его радиальную скорость. Аналогичные методы наблюдений применяются и к естественным небесным телам (например, радиолокация Венеры и Марса, лазерная локация Луны). Поэтому в середине 20 в. разработаны новые способы определения орбит, специально приспособленные для наблюдений, выполненных современными техническими средствами.
Лит.: Эскобал П. Р., Методы определения орбит, пер. с англ., М., 1970. См. также лит. при ст. Небесная механика.
  Г. А. Чеботарёв.

S — Солнце; Р — планета; П — перигелий орбиты. Ось Sx направлена в точку весеннего равноденствия." href="/a_pictures/31/13/201879305.jpg">S — Солнце; Р — планета; П — перигелий орбиты. Ось Sx направлена в точку весеннего равноденствия."http://sulphur.atomistry.com/">S — Солнце; Р — планета; П — перигелий орбиты. Ось Sx направлена в точку весеннего равноденствия." src="a_pictures/31/13/th_201879305.jpg">
Эллиптическая орбита планеты Р в пространстве: S — Солнце; Р — планета; П — перигелий орбиты. Ось Sx направлена в точку весеннего равноденствия.