Клапейрона уравнение

Значение слова "Клапейрона уравнение" в Большой Советской Энциклопедии

Клапейрона уравнение, Клапейрона — Менделеева уравнение, найденная Б. П. Э. Клапейроном (1834) зависимость между физическими величинами, определяющими состояние идеального газа: давлением газа р, его объёмом V и абсолютной температурой Т.

Клапейрона уравнение записывается в виде pV = ВТ, где коэффициент пропорциональности В зависит от массы газа. Д. И. Менделеев, используя Авогадро закон, вывел в 1874 уравнение состояния для 1 моля идеального газа pV = RT, где R — универсальная газовая постоянная. Для газа, имеющего общую массу М и молекулярную массу m,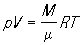

, или pV=NkT,"

где N — число частиц газа, k — Больцмана постоянная. Клапейрона уравнение представляет собой уравнение состояния, идеального газа, которое объединяет Бойля — Мариотта закон (зависимость между р и V при Т = const), Гей-Люссака закон (зависимость V от Т при р = const) и Авогадро закон (согласно этому закону, газы при одинаковых значениях р, V и Т содержат одинаковое число молекул N).

Клапейрона уравнение — наиболее простое уравнение состояния, применимое с определённой степенью точности к реальным газам при низких давлениях и высоких температурах (например, атмосферный воздух, продукты сгорания в газовых двигателях и др.), когда они близки по своим свойствам к идеальному газу.

В Большой Советской Энциклопедии рядом со словом "Клапейрона уравнение"

Клапейрон Бенуа Поль Эмиль | Буква "К" | В начало | Буквосочетание "КЛ" | Клапейрона - Клаузиуса уравнение

Статья про слово "Клапейрона уравнение" в Большой Советской Энциклопедии была прочитана 0 раз

Интересное

Florists in america

business support in USA