Конформное отображение
Определение "Конформное отображение" в Большой Советской Энциклопедии
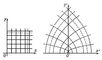
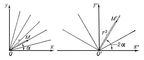
Конформное отображение, конформное преобразование (математическое), отображение одной фигуры (области) на другую, при котором две любые кривые, пересекающиеся под некоторым углом во внутренней точке первой фигуры, преобразуются в кривые второй фигуры, пересекающиеся под тем же углом. Простейший пример Конформное отображение представляет подобие. Другой пример - Конформное отображение прямого угла на полуплоскость. Его можно получить, если каждый луч, выходящий из точки О под углом a к Ox, преобразовать в луч, выходящий из O" под углом 2a к O"x", и притом так, что каждая точка М, для которой OM = r, преобразуется в точку M", для которой O"M" = r2. Т. к. М изображает комплексное число z = r (cosa + i sina), а M" - число z" = r (cos2a + isin2a) = z2, то можно сказать, что рассматриваемое Конформное отображение осуществляется посредством функции комплексного переменного z" = z2. Нетрудно убедиться в том, что полупрямые, параллельные сторонам угла, преобразуются при этом в полупараболы с общим фокусом в O".
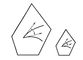
Нужно заметить, что углы с вершиной в точке О изменяются, увеличиваясь вдвое; это не противоречит определению Конформное отображение, т. к. О не является внутренней точкой области. В общем случае Конформное отображение любой криволинейный многоугольник Р, лежащий внутри отображаемой области, преобразуется в криволинейный многоугольник P" с соответственно равными углами, но длины сторон изменяются непропорционально. Если многоугольник Р уменьшается, стягиваясь в некоторую точку A, то и P" уменьшается, стягиваясь в соответствующую точку A", при этом отношения длин сторон стремятся к одному и тому же числу:
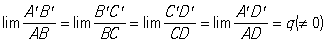 , ,
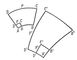
которое зависит только от положения точки А (но не от рассматриваемых многоугольников); оно называется растяжением в данной точке. Указанный факт позволяет приближённо рассматривать любое Конформное отображение «в малом» (т. е. в достаточно малой окрестности каждой точки A) как преобразование подобия, соединённое, вообще говоря, ещё с поворотом (например, четырёхугольники Р и P").
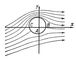
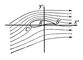
Конформное отображение применяется с давних пор в картографии, когда требуется часть поверхности земного шара изобразить на плоскости (на карте) с сохранением величин всех углов; примерами таких Конформное отображение являются стереографическая проекция и Меркатора проекция. Более общая задача Конформное отображение произвольной поверхности (или её части) на другую поверхность (или её часть) изучается в дифференциальной геометрии. Особое место занимают Конформное отображение одних областей плоскости на другие; их теория имеет существенные приложения в гидро- и аэромеханике, электростатике и теории упругости. Решение многих важных задач получается без труда, когда область, для которой ставится задача, имеет достаточно простой вид (например, круг или полуплоскость). Если задача ставится для другой, более сложной области, то оказывается достаточным отобразить конформно простейшую область на данную, чтобы получить решение новой задачи из известного решения. Так, например, задача об определении потока несжимаемой однородной жидкости или газа, обтекающего цилиндр с круговым сечением, решается сравнительно легко. Линии тока (т. е. линии, вдоль которых направлены скорости частиц жидкости), для этого случая, здесь представлено течение при наличии циркуляции. Если отобразить конформно внешность кругового сечения цилиндра на внешность поперечного сечения крыла самолёта (профиля крыла), то линии тока для случая круглого цилиндра перейдут, как можно показать, в линии тока при обтекании крыла. Знание отображающей функции z" = f (z) позволяет подсчитать скорость потока в любой точке, вычислить подъёмную силу крыла самолёта и т. д. Именно таким путём шёл Н. Е. Жуковский, создавая теорию крыла самолёта.
Не всякие области плоскости допускают Конформное отображение друг на друга. Так, например, круговое кольцо, ограниченное концентрическими окружностями радиусов R1 и R2, где R1<R2, нельзя отобразить конформно на другое кольцо, ограниченное окружностями радиусов r1 и r2, где r1<r2, если R2/R1¹r2/r1. Тем более замечательно, что любые две области, каждая из которых ограничена лишь одной кривой (односвязные области), могут быть конформно отображены друг на друга (теорема Римана). Например, любой многоугольник допускает Конформное отображение на любой другой многоугольник, а также на полуплоскость или на круг. Здесь углы на границе, вообще говоря, изменяются, но определение Конформное отображение и не требует их сохранения. Что касается областей, ограниченных несколькими кривыми, то такую область всегда можно отобразить конформно на область, ограниченную таким же числом параллельных между собой прямолинейных отрезков (теорема Гильберта) или окружностей (теорема Кёбе). Но размеры и взаимное расположение этих отрезков или окружностей нельзя задать произвольно.
Конформное отображение одной области плоскости на другую либо сохраняет направления отсчёта углов между кривыми - Конформное отображение первого рода; либо изменяет их на противоположные - К. о, второго рода. Если к любому Конформное отображение первого рода присоединить ещё зеркальное отражение относительно какой-либо прямой., то получится Конформное отображение второго рода.
Если ввести комплексные переменные z и z" в плоскостях оригинала и образа, то z", рассматриваемое при Конформное отображение как функция от z, является или аналитической функцией (Конформное отображение первого рода), или функцией, сопряжённой с аналитической (Конформное отображение второго рода). Обратно: любая функция z" = f (z), аналитическая в данной области и принимающая в разных точках области разные значения [f (z1)¹f (z2), если z1¹z2] (такая функция называется однолистной), отображает конформно данную область на некоторую область плоскости z". Поэтому изучение Конформное отображение областей плоскости сводится к изучению свойств однолистных функций.
Всякое Конформное отображение трёхмерных областей переводит сферы и плоскости в сферы и плоскости и сводится или к преобразованию подобия, или к последовательно выполненным одному преобразованию инверсии и одному преобразованию подобия (теорема Лиувилля). Вследствие этого Конформное отображение трёхмерных (и вообще многомерных) областей не имеют такого большого значения и таких разнообразных приложений, как Конформное отображение двумерных областей.
Начало теории Конформное отображение было заложено Л. Эйлером (1777), установившим значение функций комплексного переменного в задаче Конформное отображение частей сферы на плоскость (построение географических карт). Изучение общей задачи К, о. одной поверхности на другую привело в 1822 К. Гаусса к развитию общей теории поверхностей. Б. Риман (1851) установил условия, при которых возможно Конформное отображение одной области (плоскости) на другую; однако намеченное им решение удалось обосновать лишь в начале 20 в. (в трудах А. Пуанкаре и К. Каратеодори). Исследования Н. Е. Жуковского, С. А. Чаплыгина, открывших широкое поле приложений Конформное отображение в аэро- и гидромеханике, послужили мощным стимулом для развития теории Конформное отображение как большого раздела теории аналитических функций. В этой области существенное значение имеют теоретические труды отечественных учёных.
Лит.: Лаврентьев М. А., Шабат Б. В., Методы теории функций комплексного переменного, 3 изд., М., 1965; Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М., 1969; Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968: Коппенфельс В., Штальман Ф., Практика конформных отображений, пер. с нем., М., 1963.
А. И. Маркушевич.
Статья про "Конформное отображение" в Большой Советской Энциклопедии была прочитана 971 раз
|



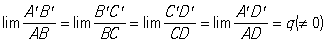 ,
,