Библиотека DJVU
БСЭ
Статистика:
Коши задача
Значение слова "Коши задача" в Большой Советской Энциклопедии
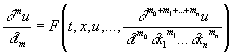, (1)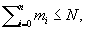
m0 < m, m > 0,удовлетворяющего т. н. начальным условиям.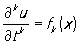
, t = t0, x Î G0, k = 0, …, m-1, (2)где G0 — носитель начальных данных — область гиперплоскости t = to пространства переменных x1,..., xn. Когда F и fk, k = 0,..., m — 1, являются аналитическими функциями своих аргументов, задача Коши (1), (2) в некоторой области G пространства переменных t, х, содержащей G0, всегда имеет и притом единственное решение. Однако это решение может оказаться неустойчивым (т. е. малое изменение начальных данных может вызвать сильное изменение решения), например в том случае, когда уравнение (1) принадлежит эллиптическому типу. При неаналитических данных задача Коши (1), (2) может потерять смысл, если не ограничиться рассмотрением того случая, когда уравнение (1) является гиперболическим.
Лит.: Курант Р., Гильберт Д., Методы математической физики, пер. с нем., т. 2, М.— Л., 1951; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.
А. В. Бицадзе.
В Большой Советской Энциклопедии рядом со словом "Коши задача"
Коши Огюстен Луи | Буква "К" | В начало | Буквосочетание "КО" | Коши интегралСтатья про слово "Коши задача" в Большой Советской Энциклопедии была прочитана 0 раз
Интересное