Кривой брус

Определение "Кривой брус" в Большой Советской Энциклопедии

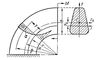Нормальное напряжение в сечении кривого бруса

Кривой брус в сопротивлении материалов и в теории упругости, тело, геометрическая форма которого образуется движением в пространстве плоской фигуры (называемом поперечным сечением К. о.), при этом центр её тяжести всегда остаётся на некоторой кривой (оси Кривой брус), а плоскость фигуры нормальна этой кривой. В зависимости от вида поперечного сечения различают: Кривой брус постоянного сечения (пример - звено цепи, составленной из овальных или круглых колец) и Кривой брус переменного сечения (пример - крюк подъёмного крана). По виду оси К, б. может быть плоским (если его ось - плоская кривая) и пространственным (ось - пространственная кривая). Разновидностью Кривой брус является естественно закрученный Кривой брус, отличающийся тем, что плоская фигура поперечного сечения при своём движении по оси Кривой брус одновременно вращается вокруг касательной к ней (пример - лопасть воздушного винта самолёта или вентилятора).

Расчёт плоского Кривой брус (рис.) симметричного поперечного сечения (ось симметрии лежит в плоскости кривизны) на действие нагрузки, лежащей в плоскости симметрии, заключается в определении напряжений (нормальных его поперечному сечению) по формуле: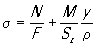
,

где F - площадь поперечного сечения, N - продольная сила, М - изгибающий момент в сечении, определяемый относительно оси z₀, проходящей через центр тяжести поперечного сечения (С), у - расстояние до рассматриваемого волокна от нейтральной оси z, r - радиус кривизны рассматриваемого волокна, S_z = Fy₀ - статический момент площади сечения относительно оси z. Смещение y₀ нейтральной оси относительно центра тяжести сечения всегда направлено к центру кривизны Кривой брус и обычно определяется по специальным таблицам. Для круглого сечения y₀ » d²/16R, для прямоугольного - у₀ » h²/12R (R - радиус кривизны оси Кривой брус, d - диаметр, h - высота поперечного сечения Кривой брус). Нормальные напряжения в Кривой брус имеют наибольшие по абсолютной величине значения у вогнутого края бруса и меняются в сечении по гиперболическому закону. При малой кривизне (R > 5h) определение нормальных напряжений может производиться, как и в прямом брусе (см. Изгиб).
 
  Лит.: Беляев Н. М., Сопротивление материалов, 14 изд., М., 1965.
  Л. В. Касабьян.