


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Лапласа уравнение
Определение "Лапласа уравнение" в Большой Советской Энциклопедии
Лапласа уравнение, дифференциальное уравнение с частными производными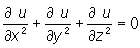
где х, у, z — независимые переменные, а u = u(x, y, z) — искомая функция. Это уравнение названо по имени П. Лапласа, рассмотревшего его в работах по теории тяготения (1782). К Лапласа уравнение приводит ряд задач физики и техники. Лапласа уравнение удовлетворяют температура при стационарных процессах, потенциал электростатического поля в точках пространства, свободных от зарядов, потенциал поля тяготения в области, не содержащей притягивающих масс, и т. п. Функции, удовлетворяющие Лапласа уравнение, называются гармоническими функциями. О постановке задач для Лапласа уравнение см. в ст. Краевые задачи.
| "БСЭ" >> "Л" >> "ЛА" >> "ЛАП" |
Статья про "Лапласа уравнение" в Большой Советской Энциклопедии была прочитана 760 раз
| Бургер двойного помола |
| Английское куриное карри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Объединённая партия гаитянских коммунистов
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная