Лоренца преобразования

Определение "Лоренца преобразования" в Большой Советской Энциклопедии

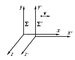Лоренца преобразования. Рис.

Лоренца преобразования, в специальной теории относительности — преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Получены в 1904 Х. А. Лоренцом как преобразования, по отношению к которым уравнения классической микроскопической электродинамики (Лоренца — Максвелла уравнения) сохраняют свой вид. В 1905 А. Эйнштейн вывел их, исходя из двух постулатов, составивших основу специальной теории относительности: равноправия всех инерциальных систем отсчёта и независимости скорости распространения света в вакууме от движения источника света.

Рассмотрим частный случай двух инерциальных систем отсчёта å и å’ с осями х и x’, лежащими на одной прямой, и соответственно параллельными другими осями (у и y’, z и z’). Если система å’ движется относительно å с постоянной скоростью u в направлении оси х, то Лоренца преобразования при переходе от å к å’ имеют вид: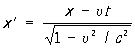
,

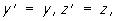
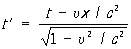
где с — скорость света в вакууме (штрихованные координаты относятся к системе å’, нештрихованные — к å).

Лоренца преобразования приводят к ряду важных следствий, в том числе к зависимости линейных размеров тел и промежутков времени от выбранной системы отсчёта, к закону сложения скоростей в теории относительности и др. При скоростях движения, малых по сравнению со скоростью света (u<<c), Лоренца преобразования переходят в преобразования Галилея (см. Галилея принцип относительности), справедливые в классической механике Ньютона.
Подробнее см. Относительности теория; см. также литературу при этой статье.
Г. А. Зисман.