


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Математическое ожидание
Определение "Математическое ожидание" в Большой Советской Энциклопедии
Математическое ожидание, среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины. Для случайной величины X, принимающей последовательность значений y1, y2, ..., yk, ... с вероятностями, равными соответственно p1, p2, ..., pk, …, Математическое ожидание определяется формулой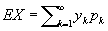
(в предположении, что ряд 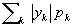 сходится). Так, например, если Х - число очков, выпадающее на верхней грани игральной кости (X принимает каждое из значений 1, 2, 3, 4, 5, 6 с вероятностью 1/6), то
сходится). Так, например, если Х - число очков, выпадающее на верхней грани игральной кости (X принимает каждое из значений 1, 2, 3, 4, 5, 6 с вероятностью 1/6), то 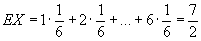 .
.
Для случайной величины, имеющей плотность вероятности р(у), Математическое ожидание определяется формулой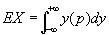 .
.
Математическое ожидание характеризует расположение значений случайной величины. Полностью эта роль Математическое ожидание разъясняется больших чисел законом. При сложении случайных величин их Математическое ожидание складываются, при умножении двух независимых случайных величин их Математическое ожидание перемножаются. Математическое ожидание случайной величины eitX, то есть f (t) = Eeitxz, где t - действительное число, носит название характеристической функции.
Лит.: Гнеденко Б. В., Курс теории вероятностей, 4 изд., М., 1965.
Ю. В. Прохоров.
| "БСЭ" >> "М" >> "МА" >> "МАТ" >> "МАТЕ" |
Статья про "Математическое ожидание" в Большой Советской Энциклопедии была прочитана 933 раз
| Коптим скумбрию в коробке |
| Буддийская молитва в Камбодже |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная